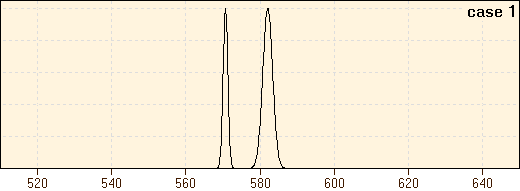
The Term "significant"

In statistics we often use the term "significance". According to my experience "significance" is used carelessly in many circumstances, and is little understood. Basically, the word "significance" comes from the Latin word significans which means "clear" or "distinct". A certain observation is thus considered to be of significance if it can be recognized easily. Speaking in more statistical terms, we connect the "level of significance" with the probability of an observation to occur. A simple example should clarify this:

Example:

Suppose that an analytical chemist determines the concentration of zinc in well water, analyzing 10 wells in the industrial north of a country, and 10 wells in the rural south. When done, the chemist calculates the means of the zinc concentration of both the northern and the southern water samples, resulting in the following values: Water in the North 570.7 µg/l Water in the South 582.1 µg/l If we pose the question whether there is a difference between the north and the south, we will certainly agree that there is a difference between the two means (at least numerically). Going further into the details, we may doubt that there is a difference, since the same values of the means may result from two entirely different scenarios: Case 1: Case 2: North South North South --------------- --------------- Water samples: 571.5 581.7 566.3 571.5 570.8 582.8 549.5 608.1 570.3 580.4 538.9 544.7 570.6 583.3 588.9 571.7 570.4 582.9 592.5 589.7 571.0 579.5 560.1 588.5 571.6 582.8 572.9 577.7 569.4 583.3 575.1 583.7 570.5 583.0 602.7 561.7 570.9 581.3 560.1 623.7 --------------- --------------- Means: 570.7 582.1 570.7 582.1 In both cases the means are 570.7 and 582.1, respectively. However, in the first case, when looking at the individual values the means will be considered to be different, in the second case this is not so obvious. If we look at the corresponding distributions, the meaning of the term significant becomes clear: on a numerical basis the difference of the means is given in both cases, however, in the first case the difference is obvious (= significant), whereas in the second case this is not evident as both distributions overlap to a very high degree.

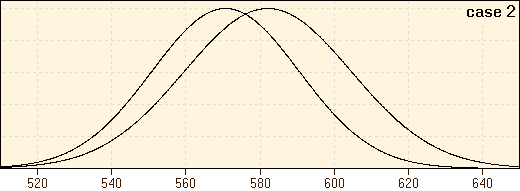
Thus, the meaning of the term significant depends on the width of the distribution of the measured values. If we abstract from this example, the term "significant" may be formulated as follows: a result is considered to be significant if the probability that it occurred by chance is low. In our example the difference of the means in the first case is evident, because the corresponding distributions do not overlap - which makes the odds that the measured values of the northern and the southern area origin from the same distribution actually zero. In the second case this probability is clearly greater than zero (i.e. 12%).

In order to make a precise statement on the significance of some results, statisticians have defined the level of significance which specifies the probability to conduct a type I error when performing statistical tests.