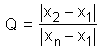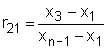Outlier Test<BR><FONT SIZE=-1>Dean and Dixon</FONT>

Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more.

Table of Contents

Statistical Tests

Outlier Tests

Dean and Dixon Test

Index

Outlier Test
Dean and Dixon

A test for outliers of normally distributed data which is particularly simple to apply has been developed by J.W. Dixon. In order to perform this test for outliers, the data set containing N values has to be sorted either in an ascending or descending order, with x₁ being the suspect value. Then the test statistic Q is calculated using the equation

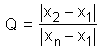
The decision whether x₁ is an outlier is performed by comparing the value Q to the critical values listed in the following table:

N	a=0.001	a=0.002	a=0.005	a=0.01	a=0.02	a=0.05	a=0.1	a=0.2
3	0.999	0.998	0.994	0.988	0.976	0.941	0.886	0.782
4	0.964	0.949	0.921	0.889	0.847	0.766	0.679	0.561
5	0.895	0.869	0.824	0.782	0.729	0.643	0.559	0.452
6	0.822	0.792	0.744	0.698	0.646	0.563	0.484	0.387
7	0.763	0.731	0.681	0.636	0.587	0.507	0.433	0.344
8	0.716	0.682	0.633	0.591	0.542	0.467	0.398	0.314
9	0.675	0.644	0.596	0.555	0.508	0.436	0.370	0.291
10	0.647	0.614	0.568	0.527	0.482	0.412	0.349	0.274
15	0.544	0.515	0.473	0.438	0.398	0.338	0.284	0.220
20	0.491	0.464	0.426	0.393	0.356	0.300	0.251	0.193
25	0.455	0.430	0.395	0.364	0.329	0.277	0.230	0.176
30	0.430	0.407	0.371	0.342	0.310	0.260	0.216	0.165

where N is the number of values and a is the level of significance.

Please note that Dean and Dixon suggested in a later paper

to take a more elaborate approach by using different formulas for different sample sizes in order to avoid the problem of two outliers on the same side of the distribution. They defined the following ratios and recommended that the various ratios be applied as follows: for 3 <= N <=7 use r₁₀; for 8 <= N <=10 use r₁₁; for 11 <= N <= 13 use r₂₁, and for n >= 14 use r₂₂:

The following tables show the critical values for r₁₁, r₂₁, and r₂₂, respectively. r₁₀ is equal to Q, its critical values can be obtained from the table above.

Critical values for r₁₁
N a=0.001 a=0.002 a=0.005 a=0.01 a=0.02 a=0.05 a=0.1 a=0.2

8 0.799 0.769 0.724 0.682 0.633 0.554 0.480 0.386

9 0.750 0.720 0.675 0.634 0.586 0.512 0.441 0.352

10 0.713 0.683 0.637 0.597 0.551 0.477 0.409 0.325

Critical values for r₂₁
N	a=0.001	a=0.002	a=0.005	a=0.01	a=0.02	a=0.05	a=0.1	a=0.2
11	0.770	0.746	0.708	0.674	0.636	0.575	0.518	0.445
12	0.739	0.714	0.676	0.643	0.605	0.546	0.489	0.420
13	0.713	0.687	0.649	0.617	0.580	0.522	0.467	0.399

Critical values for r₂₂
N	a=0.001	a=0.002	a=0.005	a=0.01	a=0.02	a=0.05	a=0.1	a=0.2
14	0.732	0.708	0.672	0.640	0.603	0.546	0.491	0.422
15	0.708	0.685	0.648	0.617	0.582	0.524	0.470	0.403
16	0.691	0.667	0.630	0.598	0.562	0.505	0.453	0.386
17	0.671	0.647	0.611	0.580	0.545	0.489	0.437	0.373
18	0.652	0.628	0.594	0.564	0.529	0.475	0.424	0.361
19	0.640	0.617	0.581	0.551	0.517	0.462	0.412	0.349
20	0.627	0.604	0.568	0.538	0.503	0.450	0.401	0.339
25	0.574	0.550	0.517	0.489	0.457	0.406	0.359	0.302
30	0.539	0.517	0.484	0.456	0.425	0.376	0.332	0.278
35	0.511	0.490	0.459	0.431	0.400	0.354	0.311	0.260
40	0.490	0.469	0.438	0.412	0.382	0.337	0.295	0.246
45	0.475	0.454	0.423	0.397	0.368	0.323	0.283	0.234
50	0.460	0.439	0.410	0.384	0.355	0.312	0.272	0.226
60	0.437	0.417	0.388	0.363	0.336	0.294	0.256	0.211
70	0.422	0.403	0.374	0.349	0.321	0.280	0.244	0.201
80	0.408	0.389	0.360	0.337	0.310	0.270	0.234	0.192
90	0.397	0.377	0.350	0.326	0.300	0.261	0.226	0.185
100	0.387	0.368	0.341	0.317	0.292	0.253	0.219	0.179

Hint: Please note that the critical values listed in the tables above have been calculated by performing 10⁶ random experiments per value. These values differ slightly from values published by various authors, many of them using interpolation techniques to estimate the critical values.

Last Update: 2005-May-08

Outlier TestDean and Dixon

Outlier Test
Dean and Dixon