| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Bivariate Data Bivariate Data  Curve Fitting Curve Fitting  Interpolation Interpolation |
|||
| See also: Extrapolation | |||
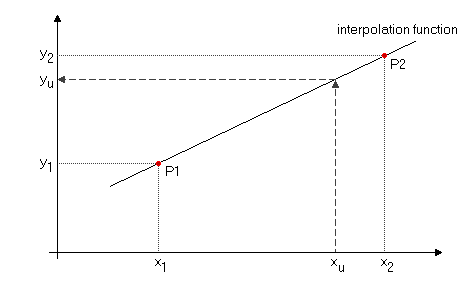
InterpolationUnter Interpolation versteht man die Abschätzung eines y-Werts für einen gegebenen x-Wert, wenn zwei oder mehrere benachbarte Punkte P1 und P2 bekannt sind. Dabei verbindet man die bekannten Punkte mit einer Funktion eines bestimmten Typs und berechnet den unbekannten y-Wert für den interessierenden x-Wert mit Hilfe dieser Funktion. Im einfachsten (und vielleicht auch häufigsten) Fall wird die Interpolationsfunktion eine Gerade sein. Genauso sind aber auch Polynome n-ter Ordnung oder andere Funktionen denkbar.
Bei linearer Interpolation errechnet sich der unbekannte y-Wert yu aus dem x-Wert xu wie folgt: yu = y1 + (xu-x1)/(x2-x1)*(y2-y1) Setzt man zur Interpolation Polynome höherer Ordnung ein, so benötigt man entsprechend mehr Referenzpunkte, da sonst die Interpolationsfunktion nicht eindeutig definiert ist. Generell gilt, dass man für ein Polynom n-ter Ordnung n+1 Punkte benötigt. Allerdings reagieren Polynome höherer Ordnung sehr stark auf kleine Abweichungen der Referenzpunkte, so dass die interpolierten Werte sehr schnell unbrauchbar werden. In vielen Fällen ist dann eine stückweise lineare Interpolation besser.
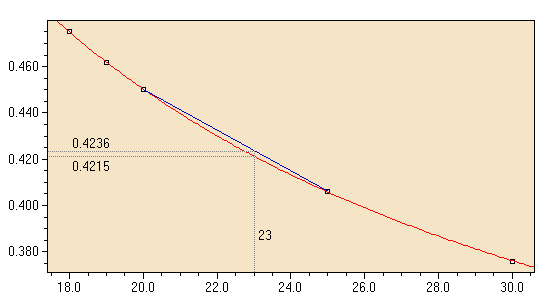
Das folgende Beispiel zeigt eine typische Interpolation, bei der aus einer Tabelle Zwischenwerte entnommen werden müssen: Angenommen, Sie führen einen Dean-Dixon-Ausreisser-Test für 23 Datenwerte auf einem Signifikanzniveau von 5% durch. Wenn Sie in der entsprechenden Tabelle nachsehen, finden Sie für N=23 keinen entsprechenden Eintrag der kritischen Grenze. Es gibt nur Werte für N=20 (0.450) und N=25 (0.406). Um nun die kritische Grenze für N=23 abzuschätzen, wenden wir eine lineare Interpolation an. Damit ergibt sich für die kritische Grenze: Interpolation bei großen Abständen zwischen den Referenzpunkten
Vorsicht ist bei der Interpolation angebracht, wenn der Abstand zu den benachbarten Referenzpunkten zu groß wird. In diesem Fall kann der Fehler bei der Interpolation so stark ansteigen, dass der interpolierte Wert nicht mehr brauchbar ist. Hier kann nur eine Approximation über einen größeren Wertebereich helfen, was allerdings voraussetzt, dass man den Zusammenhang zwischen unabhängiger und abhängiger Variable zumindest seiner Natur nach kennt (Typ der Funktion). In den meisten Fällen wird man eine passende Funktion mit Hilfe der linearen Regression parametrisieren.
|
|||
Home  Bivariate Data Bivariate Data  Curve Fitting Curve Fitting  Interpolation Interpolation |
|||