| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Basic Concepts Basic Concepts  Precision and Accuracy Precision and Accuracy  Confidence Interval Confidence Interval |
|||
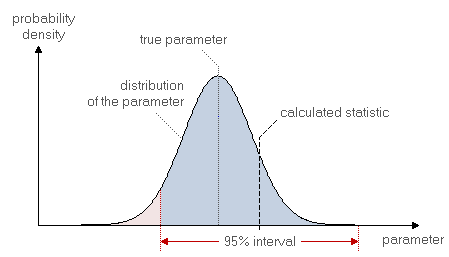
Confidence IntervalA common task in statistics is the (preferably correct) estimation of a particular parameter (e.g. the mean). While the numeric calculations of a population paramater is quite simple in most cases, the situation becomes more complicated with random samples. If we know the population the procedure is simple and clear: the parameter has to be calculated using the appropriate formula, the accuracy of the calculated value solely depends on the accuracy of the measurements and the (floating point) precision of the calculation. However, if we deal with samples, we will see that the calculated parameter (which is normally called a statistic to indicate that it has been calculated from a sample) will vary within certain limits if we calculate it from different samples of the same population. The calculated statistic will fluctuate around the true value of the parameter - which we do not know, because we do not know the population. The question which now arises is: what is the interval where the true value of the parameter will fall into, if we only know the calculated value of the corresponding statistic for a single given sample. This question cannot be answered with absolute certainty but only to a certain probability as the used sample may happen to exhibit a very large deviation which results in a calculated statistic being far off the true value of the parameter.
In order to deal with this problem of estimating a parameter from a sample we have to use probabilities. We calculate the corresponding statistic of the sample and we additionally specify a range around the statistic which includes the (unknown) true value of the parameter to a certain probability p. Usually p is set to 95%, but 99% and 99.9% are eqally good for most practical circumstances. This probability p is called confidence coefficient, the range around the sample statistic is called confidence interval.
|
|||
Home  Basic Concepts Basic Concepts  Precision and Accuracy Precision and Accuracy  Confidence Interval Confidence Interval |
|||