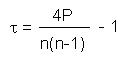| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Bivariate Data Bivariate Data  Correlation Correlation  Kendall's Tau-a Kendall's Tau-a |
|
| See also: Pearson's Correlation Coefficient | |
Kendall's Tau-aBy end of the 1930ies M. KendallLet's assume that we try to measure the relationship between two variables x and y. Kendall's algorithm is based on the idea that if there is a correlation among the two variables then sorting the data pairs [xi, yi] by one variable results in a more or less sorted series of values in the other variable. In effect, Kendall's Tau-a measures the number of sorting inversions in the variable y, given that the variable x has been sorted. If there is not a single inversion in the order of y then the two variables are 100% positively correlated, if there are exclusively inversions then the variables are 100% negatively correlated. Kendall's Tau-a is calculated according to the following formula:
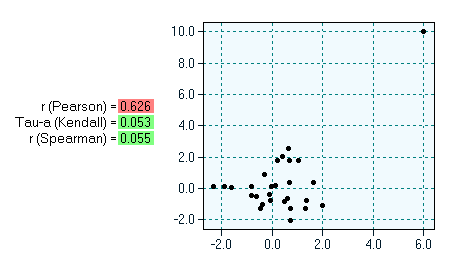
Kendall's Tau-a fails if the dataset contains a high portion of ties. In this case one should use either Kendall's Tau-b/Tau-c, or Kruskal's Gamma. The advantage of Kendall's Tau-a over the "classic" Pearson's correlation coefficient can be seen in the following example. The diagram below shows 28 data pairs, of which 27 are uncorrelated and one pair obviously constitutes an outlier. Outliers in bivariate settings always result in high correlations values (if one uses Pearson's correlation coefficient). Kendall's Tau-a, however, is immune against outliers (similar to Spearman's rank coefficient).
|
|
Home  Bivariate Data Bivariate Data  Correlation Correlation  Kendall's Tau-a Kendall's Tau-a |
|