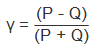| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Bivariate Data Bivariate Data  Correlation Correlation  Kruskal's Gamma Kruskal's Gamma |
|||||||
Goodman and Kruskal's GammaGoodman and Kruskal's gamma (or gamma, for short) is a symmetric measure of association (correlation) which delivers values in the range of -1.0 to +1.0. The idea behind gamma is to measure the relative difference of concordant and discordant(1) pairs in a sorted list of paired observations (ignoring ties). If the number of concordant pairs is P, and the number of discordant pairs is denoted by Q, then gamma is calculated according to the following formula:
Goodman and Kruskal's gamma is approximately normally distributed for large samples. Thus it is possible to calculate p-values and/or a level of significance.
|
|||||||
Home  Bivariate Data Bivariate Data  Correlation Correlation  Kruskal's Gamma Kruskal's Gamma |
|||||||