| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Bivariate Daten Bivariate Daten  Korrelation Korrelation  Einleitung Einleitung |
|
| Siehe auch: Autokorrelation, Korrelation - Challenger-Desaster, Pearsons Korrelationskoeffizient, Kovarianz, Streu-, Kovarianz- und Korrelationsmatrix | |
| Search the VIAS Library | Index | |
|
KorrelationAuthor: Hans Lohninger
Das Ziel der Korrelationsanalyse ist, Beziehungen zwischen Variablen zu entdecken. Dabei ist es wichtig, dass mit der Bezeichnung "Korrelation" normalerweise eine lineare Korrelation gemeint ist. Als Maß für die (lineare) Korrelation wird meist der Korrelationskoeffizient verwendet. Die Bedeutung der Korrelation wird manchmal überbewertet, denn ein hoher Korrelationskoeffizient bedeutet nicht immer eine hohe Korrelation. Doch ein Korrelationskoeffizient von null bedeutet notwendigerweise auch nicht, dass es keinerlei Beziehung zwischen zwei Variablen gibt: Die linke Abbildung zeigt einen unkorrelierten Datensatz, während die rechte Abbildung eine perfekte parabolische Beziehung zeigt, obwohl der Korrelationskoeffizient in beiden Fällen nahe null ist. 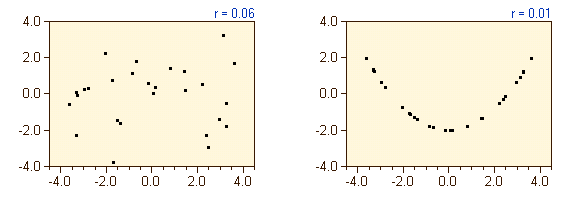 Umgekehrt muss ein hoher Korrelationskoeffizient nicht unbedingt einer hohen Korrelation zwischen den Daten zuzuschreiben sein (wie in der Abbildung links unten), sondern kann auch auf einen einzelnen Ausreißer, der abseits des unkorrelierten Rests der Datenpunkte liegt, zurückzuführen sein (rechts unten). 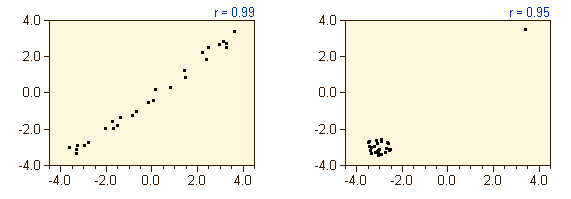 Im allgemeinen sollte man parallel zur Berechnung der Korrelation immer auch einen Blick auf den zugehörigen Streuplot werfen, um Fehlinterpretationen zu vermeiden. Weitere Beispiele zur Korrelation, die aus realen Datensätzen stammen, finden Sie hier.
|
|
Home  Bivariate Daten Bivariate Daten  Korrelation Korrelation  Einleitung Einleitung |
|
Last Update: 2013-10-17

