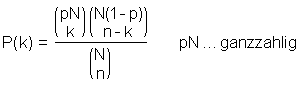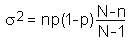| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Univariate Daten Univariate Daten  Verteilungen Verteilungen  Die wichtigsten Verteilungen Die wichtigsten Verteilungen  Diskrete Verteilungen Diskrete Verteilungen  Hypergeometrische Verteilung Hypergeometrische Verteilung |
|||||||||||||
| Siehe auch: Binomialverteilung, Beziehungen zwischen Verteilungen, Bernoulli-Verteilung | |||||||||||||
| Search the VIAS Library | Index | |||||||||||||
|
Hypergeometrische VerteilungAuthor: Hans Lohninger
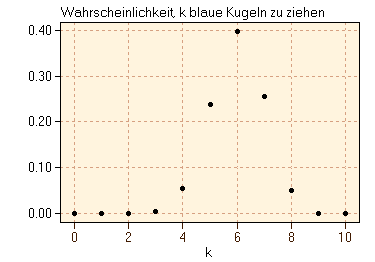
Die hypergeometrische Verteilung ist eine diskrete Verteilung und wird verwendet, um die Wahrscheinlichkeit zu beschreiben, k Beobachtungen der Klasse 1 zu finden, wenn n Proben aus einer Grundgesamtheit von N Objekten gezogen worden sind und die Wahrscheinlichkeit eines einzelnen Elements der Klasse 1 gleich p ist.
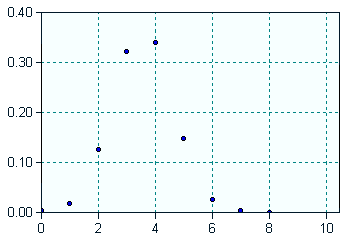
BeispielNehmen wir an, wir haben 20 Kugeln in einem Sack, von denen 8 blau sind und 12 rot. Nun mischen wir die Kugeln und ziehen 15 Kugeln. Wie groß ist die Wahrscheinlichkeit, genau 5 blaue und 10 rote Kugeln zu ziehen? Die Antwort auf diese Frage wird durch die hypergeopmetrische Verteilung gegeben:
N = 20
|
|||||||||||||
Home  Univariate Daten Univariate Daten  Verteilungen Verteilungen  Die wichtigsten Verteilungen Die wichtigsten Verteilungen  Diskrete Verteilungen Diskrete Verteilungen  Hypergeometrische Verteilung Hypergeometrische Verteilung |
|||||||||||||
Last Update: 2012-10-08