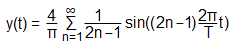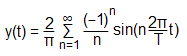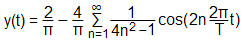| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Bivariate Daten Bivariate Daten  Zeitserien Zeitserien  Fouriertransformation Fouriertransformation  Fourier-Reihen Fourier-Reihen |
|||||||||||||||
| Siehe auch: Fourier-Transformation - Einführung, Fast-Fourier-Transformation | |||||||||||||||
| Search the VIAS Library | Index | |||||||||||||||
|
Fourier-ReihenAuthor: Hans Lohninger
Jedes periodische Signal y(t) kann als unendliche Summe von Sinus- und Kosinustermen dargestellt werden. Diese Summe wird Fourier-Reihe genannt:
Die Menge an Kosinus- und Sinusfunktionen ist komplett und orthogonal, was garantiert, dass jede periodische Funktion y(t) repräsentiert werden kann und dass die Fourier-Koeffizienten voneinander unabhängig sind. Der Index n in den obigen Formeln kann jeweils einer bestimmten Frequenz fn zugeordnet werden:
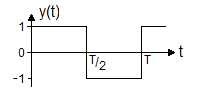
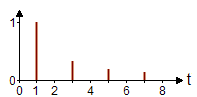
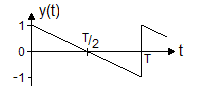
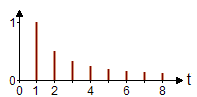
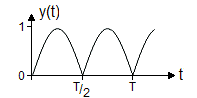
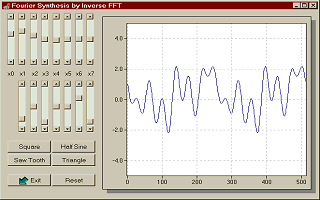
fn = n In der Praxis wird man aber meist auf die Amplitude und die Phase zurückgreifen und bekommt so das Amplitudenspektrum und das Phasenspektrum. Trägt man die quadrierte Amplitude gegen die Frequenz auf, so erhält man das Leistungsspektrum. Beispiele von Fourier-ReihenDie folgende Tabelle zeigt ein paar Beispiele einfacher periodischer Funktionen. Die dargestellten Amplitudenspektren sind so normiert, dass die höchsten Spektrallinien jeweils 1.0 lang sind und berücksichtigen nicht die tatsächlichen Signalamplituden.
|
|||||||||||||||
Home  Bivariate Daten Bivariate Daten  Zeitserien Zeitserien  Fouriertransformation Fouriertransformation  Fourier-Reihen Fourier-Reihen |
|||||||||||||||
Last Update: 2012-10-19


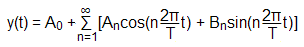
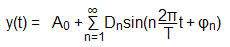
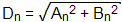
 f0
f0