Fensterfunktionen in der FFT

Author: Hans Lohninger

FFT-basierte Messungen leiden im Allgemeinen unter einem Phänomen, das man als "Leackage" (oder "Lecken") bezeichnet. Darunter versteht man die Verbreiterung der Spektrallinien und das Auftauchen von Seitenbändern wenn die Frequenz der untersuchten Schwingung(en) nicht ein ganzzahliges Vielfaches des inversen Messintervalls ist (d.h., dass eine Unstetigkeit entstehen würde, wenn man die Messdaten im Messfenster kopieren und die beiden Fenster aneinander reihen würde).

Bei der Berechnung der FFT wird implizit angenommen, dass das Signal innerhalb des Datenblocks (dessen Länge meist eine Potenz von 2 ist) periodisch ist und das Signal durch Aneinanderreihung des Datenblocks unendlich oft wiederholt wird. Das bedeutet unmittelbar, dass eine Unstetigkeit auftritt, falls sich die Signalpegel und die ersten Ableitungen am linken und rechten Ende des Datenblocks unterscheiden.

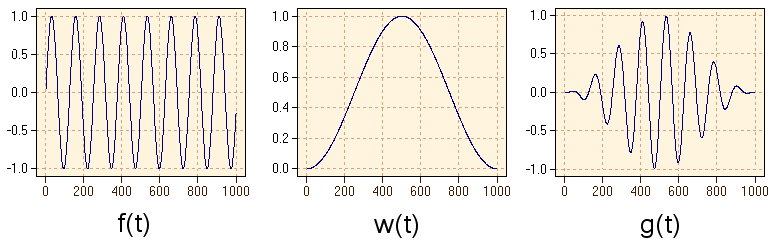
Diese Unstetigkeit führt im Spektrum zu einer Aufweitung der Spektrallinien und zum Auftauchen von neuen Spektrallinien. Um dieses Phänomen zu unterdrücken, kann man die Zeitserie mit einer Gewichtungsfunktion ("Fensterfunktion") multiplizieren. Verzichtet man auf diese Gewichtung, so entspricht das der Multiplikation mit einer Rechteckfunktion, dessen Breite dem Messintervall entspricht.

Wirkungsweise einer Fensterfunktion: die Sinus-Funktion f(t) wird mit einem Hanning-Fenster w(t) multipliziert, wodurch sich die Funktion g(t) ergibt. Diese wird dann der Fourieranalyse unterworfen.

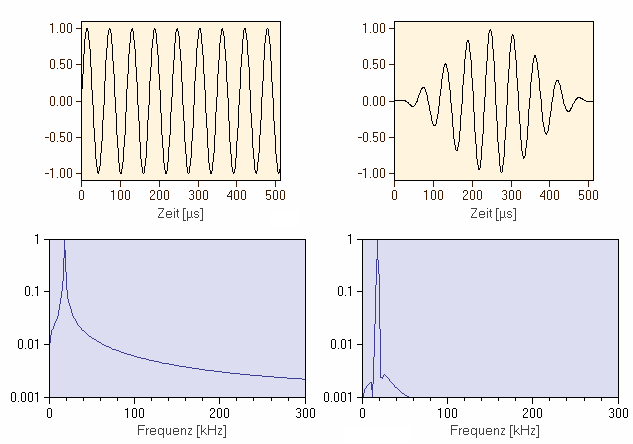
Berechnet man die Fouriertransformation der gewichteten Daten, so sieht man, dass die Spektrallinien wieder entsprechend schmäler werden. In der folgenden Abbildung ist links das ungewichtete Spektrum zu sehen, rechts das gewichtete:

Eine Multiplikation im Ortsraum entspricht im Fourierraum einer Faltungsoperation. Für die Multiplikation mit einer Rechteckfunktion im Ortsraum ergibt im Fourierraum eine Faltung mit der sinc-Funktion.

Die Auswahl einer geeigneten Fensterfunktion ist immer ein Kompromiss zwischen Seitenbandunterdrückung und Breite der Spektrallinien. Die folgende Tabelle gibt die Funktionen der wichtigsten Gewichtungsfenster an:

Name	Funktion
Rechteckfenster (= keine Gewichtungsfunktion)	F(x) = 1 for |x| <= N F(x) = 0 for |x| > N
Dreiecksfenster (Bartlett-Fenster)	F(x) = 1 - |x|/N for |x| <= N F(x) = 0 for |x| > N
Cosinus-Glockenfenster (oder Hanning-Fenster)	F(x) = cos2(x/N)
Gauss'sches Fenster	F(x) = exp(-(αx/N)2)
Hamming-Fenster	F(x) = 0.54 + 0.46*cos(x/N)
Blackman-Fenster	F(x) = 0.42 + 0.50*cos(x/N) + 0.08*cos(2x/N)
Blackman-Harris-Fenster	F(x) = 0.359 + 0.488*cos(x/N) + 0.141*cos(2x/N) + 0.012*cos(2x/N)
Blackman-Nuttall-Fenster	F(x) = 0.364 + 0.489*cos(x/N) + 0.137*cos(2x/N) + 0.011*cos(2x/N)

Das Cosinus-Glockenfenster, das Hamming-Fenster und das allgemeine Tukey-Fenster sind eng miteinander verwandt, wobei das Tukey-Fenster wie folgt definiert ist:

F(x) = 1-2α+2α*cos(x/N)

Der Parameter α bestimmt die Art des Fensters:

Hamming-Fenster: α = 0.23
Hanning-Fenster: α = 0.25

Verschiedene, in der Signalverarbeitung gebräuchliche Fensterfunktionen: Das Rechteck-, Dreieck-, Hanning-, und Welch-Fenster, berechnet für eine Fensterbreite von 1000 Datenpunkten.