Fourier-Transformation - Einführung

Author: Hans Lohninger

Die Fourier-Transformation ermöglicht es, ein Signal von einer Darstellung in der Zeitdomäne (in der es meistens gemessen wird) zu einer Darstellung in der Frequenzdomäne umzuwandeln. Die Fourier-Transformation ist reversibel; deshalb ist es möglich, beide Darstellungen zur Verarbeitung eines Signals zu wählen. Die Fourier-Transformation ergibt sich aus der Verallgemeinerung der Fourier-Reihen auf ein unendliches Intervall:

mit der ausreichenden Bedingung:

Um ein Signal in die Zeitdomäne zurückzutransformieren, wird die inverse Fourier-Transformation angewendet: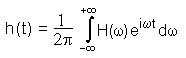

Ersetzt man das Integral durch die Summe, erhält man die diskrete Fourier-Transformation (DFT), die auf digitalisierte Daten angewendet werden kann:

Bei der praktischen Anwendung der Fourier-Transformation tritt ein gravierendes Problem auf: Sie benötigt zu viel Rechenleistung, um in Echtzeit ausgeführt werden zu können. Doch es gibt eine Familie von äquivalenten Algorithmen, die ursprünglich von Runge, Danielson und Lanczos entwickelt wurden und sehr viel schneller als der originale DFT-Algorithmus sind. J.W. Cooley hat diese Technik wiederentdeckt, die seitdem Fast-Fourier-Transformation (FFT) genannt wird.