Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu.

Home Mathematischer Hintergrund Matrizen Determinanten Determinante einer Matrix
Siehe auch: Determinanten einer Matrix 2. und 3. Ordnung, Rang einer Matrix 
 
Search the VIAS Library  |  Index


Determinante der Matrix

Author: Hans Lohninger

Neben dem Rang einer Matrix ist auch die Determinante eine wichtige charakteristische Zahl der Matrix. Die Determinante einer Matrix A wird als |A| geschrieben. Um die Definition einer Determinante zu verstehen, müssen wir uns zunächst mit dem Begriff der Permutation beschäftigen:

Permutation (n1, n2, n3 ... nk) sei eine geordnete Menge von k beliebigen Zahlen. Jede geordnete Anordnung derselben Zahlen, z.B. (np1, np2, np3 ... npk) wird als Permutation dieser Menge bezeichnet. In unserem Fall gegeben durch p.
Ungerade (gerade) Permutation Jeder Fall, in dem in einer Permutation (p1, p2, p3 ... pk) von (1, 2, 3 ... k) ps pr vorangeht und größer ist als pr, wird als Inversion dieser Permutation p bezeichnet. p gilt als ungerade oder gerade, je nachdem, ob die Zahl der Inversionen gerade oder ungerade ist.

Beispiel einer ungeraden Permutation:
(3, 1, 4, 2) ist eine Permutation von (1, 2, 3, 4). Die Zahl 3 hat in dieser Permutation zwei Inversionen: Sie geht 1 und 2 voraus und ist größer als 1 und 2. Sie geht auch 4 voraus, ist aber kleiner als 4, daher kann das nicht gezählt werden. 1 hat keine Inversionen, jedoch geht 4 der 2 voraus. Wir erhalten daher 2+0+1+0 = 3 Inversionen, also ist die Permutation (3, 1, 4, 2) ungerade.

Nach diesen Definitionen über Permutationen können wir die Determinante einer Matrix wie folgt definieren:

Determinante einer Matrix Wenn A eine beliebige quadratische Matrix ist, dann ist ihre Determinante (geschrieben als |A|) die Summe der Produkte aller Permutationen aller Elemente in jeder beliebigen Zeile, multipliziert entweder mit +1 oder mit -1, je nachdem, ob die entsprechende Permutation gerade oder ungerade ist.

Beachten Sie, dass Determinanten nur für quadratische Matrizen definiert sind und dass die Determinante einer quadratischen Matrix und ihrer transponierten Matrix gleich ist. Es gibt eine wichtige Beziehung dem Produkt von (quadratischen) Matrizen und ihren Determinanten:

Produkt von Determinanten A, B und C seien quadratische Matrizen derselben Ordnung. Wenn C = AB, dann ist |C|=|A||B|.

Die Bedeutung der Determinanten

Eine wichtige Regel bei Determinanten ist, dass |A| immer 0 ist, wenn mindestens zwei Vektoren einer Matrix linear abhängig sind. In diesem Fall ist der Rang einer Matrix gewöhnlich das bessere Maß, da er zusätzlich die Information liefert, wie viele Vektoren abhängig sind. In praktischen Situationen können die Vektoren einer Matrix im formalen Sinn linear unabhängig sein, aber einander sehr ähnlich, was in einer "beinahen Abhängigkeit" resultiert. Solche Situationen können sich in einer numerischen Instabilität äußern und müssen festgestellt werden.

Gewöhnlich wird die Determinante mit zunehmender Unabhängigkeit der Vektoren, die die Matrix bilden, größer. Tatsächlich definiert die Determinante das Volumen einer geometrischen Form, die durch die Vektoren der Matrix aufgespannt wird. Je "ähnlicher" sich die Vektoren werden (d.h., dass sie in dieselbe Richtung zeigen), desto kleiner wird das Volumen.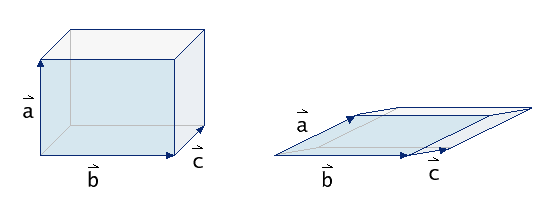


Für nicht quadratische Matrizen kann gezeigt werden, dass immer einige Vektoren (entweder Zeilen oder Spalten) abhängig von anderen Vektoren sind. Daher können wir die Determinante solcher nicht quadratischen Matrizen immer mit null festlegen.

Home Mathematischer Hintergrund Matrizen Determinanten Determinante einer Matrix

Last Update: 2012-10-08