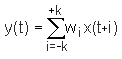| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Bivariate Daten Bivariate Daten  Glättung Glättung  Gleitender Mittelwert Gleitender Mittelwert |
|
| Siehe auch: Savitzky-Golay-Filter | |
| Search the VIAS Library | Index | |
|
Gleitender MittelwertAuthor: Hans Lohninger
Der gleitende Mittelwert (manchmal auch gleitender Durchschnitt genannt) ist eine einfache Methode zur Glättung von Messdaten. Dabei werden die Datenpunkte durch den arithmetischen Mittelwert der Nachbarpunkte (oder einer gewichteten Form davon) ersetzt. Im einfachsten Fall geschieht dies durch Mittelung von drei Datenpunkten (der ausgewählte Datenpunkt und seine beiden Nachbarn): Das Fenster, in dem die Mittelung erfolgt, wird über die Daten bewegt und nach jeder Berechnung um einen Wert nach rechts verschoben, daher die Bezeichnung gleitender Mittelwert. Der gleitende Mittelwert kann allgemein durch
beschrieben werden, wobei 2k+1 die Größe des beweglichen Fensters angibt, Die Gewichte wi sind im einfachsten Fall alle gleich 1.0 - was dem arithmetischen Mittelwert entspricht. Man kann die Gewichte aber auch so einstellen, dass z.B. Randwerte weniger Einfluss auf das Ergebnis haben als der zentrale Wert (man spricht dann von einem gewichteten Mittelwert). Da der gleitende Mittelwert in der oben angeführten Definition immer auch einen Zugriff auf zukünftige Einzelwerte benötigt, kann er nur offline berechnet werden. Setzt man den gleitenden Mittelwert zur Echtzeitberechnung ein (ber der man ja nur die Vergangenheit und Gegenwart kennt), so bleibt der Algorithmus zwar der selbe, man verwendet aber ein Fenster, das nur vergangene Punkte enthält; der letzte Wert im Fenster entspricht dann der Gegenwart, alle anderen Punkte liegen in der Vergangenheit. Dies führt aber zu einer Verschiebung des geglätteten Datenstroms um (k-1)/2. Eine "klassische" Anwendung des (verschobenen) geglätteten Mittelwerts besteht in den vielfältigen Mittelwertskurven, die man in Grafiken zu Börsenkursen findet, und die von vielen Börsenteilnehmern zu einer Aussage über die Zukunft (nämlich die Entscheidung zu kaufen oder zu verkaufen) herangezogen werden (ob das nun wirklich klug ist, wagt der Autor zu bezweifeln). Beachten Sie, dass der gleitende Mittelwert in engem Zusammenhang mit dem Savitzky-Golay-Filter und dem FIR-Filter steht. Der gleitende Mittelwert entspricht einem Tiefpassfilter in der Signalverarbeitung, das heißt hohe Frequenzanteile werden gedämpft, während tiefe Frequenzen unverändert bleiben.
|
|
Home  Bivariate Daten Bivariate Daten  Glättung Glättung  Gleitender Mittelwert Gleitender Mittelwert |
|
Last Update: 2012-10-08