| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Statistische Tests Statistische Tests  Ausreissertests Ausreissertests  Ausreissertests - Grundregeln Ausreissertests - Grundregeln |
|
| Siehe auch: Ausreißer, Verteilungsrechner, Theorem von Chebyshev (Tschebyscheff) | |
| Search the VIAS Library | Index | |
|
Ausreißertests - GrundregelnAuthor: Hans Lohninger
Basierend auf der StandardabweichungWenn wir eine Normalverteilung annehmen, kann ein einzelner Wert als Ausreißer betrachtet werden, wenn er außerhalb eines bestimmten Bereichs der Standardabweichung liegt. In vielen Fällen wird ein Faktor von 2,5 verwendet, was besagt, dass ungefähr 99 % der Daten einer Normalverteilung in diesen Bereich fallen:
Gehören die Datenwerte nicht zu einer Normalverteilung, muss die Auswahl der Grenzwerte für die Ausreißer vorsichtiger erfolgen. Nach dem Theorem von Tschebyscheff muss ein Intervall von +/- 4 Standardabweichungen verwendet werden, um sicherzustellen, dass zumindest 94 % der Daten (einer beliebigen Verteilung) in dieses Intervall fallen (bei Vorliegen einer Normalverteilung umfasst ein Intervall von +/-4s 99.99% der Daten). Beachten Sie bitte, dass diese grundsätzlichen Tests mindestens 10 Messwerte (besser 25 oder mehr) erfordern. Basierend auf dem Interquartilsabstand Die oben angeführten Methoden zur Identifizierung eines Ausreißers sind für symmetrische und unimodale Verteilungen am besten geeignet. Bei schiefen Verteilungen, empfiehlt es sich, den Grenzwert für Ausreißer aus dem Interquartilsabstand zu berechnen: x0.25 - 1.5 [x0.75 - x0.25] < xi < x0.75 + 1.5 [x0.75 - x0.25]
|
|
Home  Statistische Tests Statistische Tests  Ausreissertests Ausreissertests  Ausreissertests - Grundregeln Ausreissertests - Grundregeln |
|
Last Update: 2012-10-08


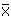 +/- 2.5σ
+/- 2.5σ