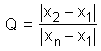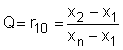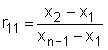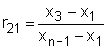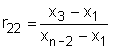|
Dean-Dixon Ausreißertest
Author: Hans Lohninger
Ein Ausreißertest für normalverteilte Daten, der besonders einfach anzuwenden ist, wurde von J.W. Dixon  entwickelt. Dieser Test eignet sich hervorragend für kleinere Stichprobenumfänge; ab etwa 30 Proben kann man den Signifikanztest nach Pearson und Hartley einsetzen. Um den Test anzuwenden, muss der Datensatz mit N Werten zuerst entweder in aufsteigender oder absteigender Reihenfolge geordnet werden, mit x1 als zu prüfendem Wert. Dann wird die
Testgröße Q nach folgender Formel berechnet: entwickelt. Dieser Test eignet sich hervorragend für kleinere Stichprobenumfänge; ab etwa 30 Proben kann man den Signifikanztest nach Pearson und Hartley einsetzen. Um den Test anzuwenden, muss der Datensatz mit N Werten zuerst entweder in aufsteigender oder absteigender Reihenfolge geordnet werden, mit x1 als zu prüfendem Wert. Dann wird die
Testgröße Q nach folgender Formel berechnet:
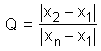
Die Entscheidung, ob x1 ein Ausreißer ist, wird durch Vergleich des Werts Q mit den kritischen Werten aus folgender Tabelle entschieden (N ist die Anzahl der Werte, α ist das Signifikanzniveau). Falls der Wert von Q größer als der kritische Wert ist, handelt es sich bei x1 um einen Ausreißer:
| N | α=0.001 | α=0.002 | α=0.005 | α=0.01 | α=0.02 | α=0.05 | α=0.1 | α=0.2 |
| 3 | 0.999 | 0.998 | 0.994 | 0.988 | 0.976 | 0.941 | 0.886 | 0.782 |
| 4 | 0.964 | 0.949 | 0.921 | 0.889 | 0.847 | 0.766 | 0.679 | 0.561 |
| 5 | 0.895 | 0.869 | 0.824 | 0.782 | 0.729 | 0.643 | 0.559 | 0.452 |
| 6 | 0.822 | 0.792 | 0.744 | 0.698 | 0.646 | 0.563 | 0.484 | 0.387 |
| 7 | 0.763 | 0.731 | 0.681 | 0.636 | 0.587 | 0.507 | 0.433 | 0.344 |
| 8 | 0.716 | 0.682 | 0.633 | 0.591 | 0.542 | 0.467 | 0.398 | 0.314 |
| 9 | 0.675 | 0.644 | 0.596 | 0.555 | 0.508 | 0.436 | 0.370 | 0.291 |
| 10 | 0.647 | 0.614 | 0.568 | 0.527 | 0.482 | 0.412 | 0.349 | 0.274 |
| 15 | 0.544 | 0.515 | 0.473 | 0.438 | 0.398 | 0.338 | 0.284 | 0.220 |
| 20 | 0.491 | 0.464 | 0.426 | 0.393 | 0.356 | 0.300 | 0.251 | 0.193 |
| 25 | 0.455 | 0.430 | 0.395 | 0.364 | 0.329 | 0.277 | 0.230 | 0.176 |
| 30 | 0.430 | 0.407 | 0.371 | 0.342 | 0.310 | 0.260 | 0.216 | 0.165 |
Man beachte, dass Dean und Dixon in einer späteren Publikation  einen etwas komplexeren Ansatz vorgeschlagen haben, um das Problem von zwei Ausreißern auf der selben Seite der Verteilung besser in den Griff zu bekommen. Sie haben folgende neue Testgrößen entwickelt und empfahlen, die verschiedenen Testgrößen wie folgt einzusetzen: für 3 <= N <=7 wird r10 benutzt; für 8 <= N <=10 wird r11 eingesetzt; für 11 <= N <= 13 benutzt man r21, und für n >= 14 wird r22 eingesetzt. einen etwas komplexeren Ansatz vorgeschlagen haben, um das Problem von zwei Ausreißern auf der selben Seite der Verteilung besser in den Griff zu bekommen. Sie haben folgende neue Testgrößen entwickelt und empfahlen, die verschiedenen Testgrößen wie folgt einzusetzen: für 3 <= N <=7 wird r10 benutzt; für 8 <= N <=10 wird r11 eingesetzt; für 11 <= N <= 13 benutzt man r21, und für n >= 14 wird r22 eingesetzt.
Die folgenden Tabellen zeigen die kritischen Werte für r11, r21, und r22. r10 ist gleich Q, dessen kritische Werte in der Tabelle oben aufgelistet sind.
Kritische Werte für r11
| N | α=0.001 | α=0.002 | α=0.005 | α=0.01 | α=0.02 | α=0.05 | α=0.1 | α=0.2 |
| 8 | 0.799 | 0.769 | 0.724 | 0.682 | 0.633 | 0.554 | 0.480 | 0.386 |
| 9 | 0.750 | 0.720 | 0.675 | 0.634 | 0.586 | 0.512 | 0.441 | 0.352 |
| 10 | 0.713 | 0.683 | 0.637 | 0.597 | 0.551 | 0.477 | 0.409 | 0.325 |
Kritische Werte für r21
| N | α=0.001 | α=0.002 | α=0.005 | α=0.01 | α=0.02 | α=0.05 | α=0.1 | α=0.2 |
| 11 | 0.770 | 0.746 | 0.708 | 0.674 | 0.636 | 0.575 | 0.518 | 0.445 |
| 12 | 0.739 | 0.714 | 0.676 | 0.643 | 0.605 | 0.546 | 0.489 | 0.420 |
| 13 | 0.713 | 0.687 | 0.649 | 0.617 | 0.580 | 0.522 | 0.467 | 0.399 |
Kritische Werte für r22
| N | α=0.001 | α=0.002 | α=0.005 | α=0.01 | α=0.02 | α=0.05 | α=0.1 | α=0.2 |
| 14 | 0.732 | 0.708 | 0.672 | 0.640 | 0.603 | 0.546 | 0.491 | 0.422 |
| 15 | 0.708 | 0.685 | 0.648 | 0.617 | 0.582 | 0.524 | 0.470 | 0.403 |
| 16 | 0.691 | 0.667 | 0.630 | 0.598 | 0.562 | 0.505 | 0.453 | 0.386 |
| 17 | 0.671 | 0.647 | 0.611 | 0.580 | 0.545 | 0.489 | 0.437 | 0.373 |
| 18 | 0.652 | 0.628 | 0.594 | 0.564 | 0.529 | 0.475 | 0.424 | 0.361 |
| 19 | 0.640 | 0.617 | 0.581 | 0.551 | 0.517 | 0.462 | 0.412 | 0.349 |
| 20 | 0.627 | 0.604 | 0.568 | 0.538 | 0.503 | 0.450 | 0.401 | 0.339 |
| 25 | 0.574 | 0.550 | 0.517 | 0.489 | 0.457 | 0.406 | 0.359 | 0.302 |
| 30 | 0.539 | 0.517 | 0.484 | 0.456 | 0.425 | 0.376 | 0.332 | 0.278 |
| 35 | 0.511 | 0.490 | 0.459 | 0.431 | 0.400 | 0.354 | 0.311 | 0.260 |
| 40 | 0.490 | 0.469 | 0.438 | 0.412 | 0.382 | 0.337 | 0.295 | 0.246 |
| 45 | 0.475 | 0.454 | 0.423 | 0.397 | 0.368 | 0.323 | 0.283 | 0.234 |
| 50 | 0.460 | 0.439 | 0.410 | 0.384 | 0.355 | 0.312 | 0.272 | 0.226 |
| 60 | 0.437 | 0.417 | 0.388 | 0.363 | 0.336 | 0.294 | 0.256 | 0.211 |
| 70 | 0.422 | 0.403 | 0.374 | 0.349 | 0.321 | 0.280 | 0.244 | 0.201 |
| 80 | 0.408 | 0.389 | 0.360 | 0.337 | 0.310 | 0.270 | 0.234 | 0.192 |
| 90 | 0.397 | 0.377 | 0.350 | 0.326 | 0.300 | 0.261 | 0.226 | 0.185 |
| 100 | 0.387 | 0.368 | 0.341 | 0.317 | 0.292 | 0.253 | 0.219 | 0.179 |
| Hinweis: |
Die kritischen Werte in den Tabellen oben wurden von Grund auf neu berechnet, in dem pro Wert 106 Zufallsexperimente durchgeführt wurden. Diese Werte unterscheiden sich manchmal leicht von Werten, die von anderen Autoren publiziert wurden, die in vielen Fällen die kritischen Werte durch Interpolation geschätzt haben.
|
|


 Statistische Tests
Statistische Tests  Ausreissertests
Ausreissertests  Ausreissertests nach Dean und Dixon
Ausreissertests nach Dean und Dixon Statistische Tests
Statistische Tests  Ausreissertests
Ausreissertests  Ausreissertests nach Dean und Dixon
Ausreissertests nach Dean und Dixon