Rechenregeln für Wahrscheinlichkeiten

Author: Hans Lohninger

Die Berechnung der Wahrscheinlichkeiten von Ereignissen ist eng mit den Gesetzen der Mengenlehre verknüpft. Wir müssen deshalb die wichtigsten Regeln für die Berechnung der Wahrscheinlichkeit von bestimmten Mengenoperationen spezifizieren. Diese Regeln basieren auf den Axiomen von Kolmogorow:

Axiome von Kolmogorow

Jedes Ergebnis eines Zufallsexperiments A hat eine Wahrscheinlichkeit p(A), die durch die folgenden Beziehungen beschrieben wird: (1) 0 <= p(A) <= 1. (2) Wenn W der Stichprobenraum ist, folgt p(W) = 1. (3) Für eine endliche oder unendliche Reihe von disjunkten (sich nicht überlappenden) Ereignissen Ai ist die Gesamtwahrscheinlichkeit die Summe aller Wahrscheinlichkeiten der einzelnen Ereignisse Ai.

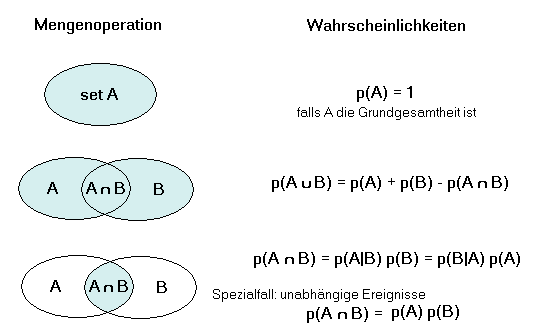
Aus diesen Axiomen können diese wichtigen Gleichungen hergeleitet werden:

Unabhängige Ereignisse: Die Ereignisse A und B sind unabhängig, wenn das Auftreten von B die Wahrscheinlichkeit von A nicht verändert und umgekehrt. Die bedingte Wahrscheinlichkeit p(A|B) ist für unabhängige Ereignisse gleich p(A).