|
Skalenniveau
Author: Hans Lohninger
Variablen sind oft nicht nur Zahlen, sie können auch qualitative Attribute einschließen. Daraus ergeben sich unterschiedliche Skalenniveaus (auch Messniveaus genannt), wobei nach Stevens  und Conover und Conover  vier Arten von Skalen unterschieden werden können: vier Arten von Skalen unterschieden werden können:
- Nominalskala: Diese Skala basiert auf einem Satz von qualitativen Attributen. Es existiert kein Kriterium, nach dem die Punkte einer nominal skalierten Variablen anzuordnen sind. Lediglich der direkte Vergleich ("ist gleich" und "ist nicht gleich") ist möglich und erlaubt. Beispiele: Tierarten, Geschlecht, die Nummern auf den Dressen der Fußballspieler. Ein nominal skaliertes Merkmal mit nur zwei Ausprägungsarten wird dichotomes Merkmal 1) genannt.
- Ordinalskala: Diese Skala bezieht sich auf Messungen, die mit "größer", "kleiner" oder "gleich" geordnet werden können. Die Beobachtungen müssen nicht gleichen Abstand aufweisen. Eine Ordinalskala erlaubt die Objekte in eine Reihenfolge zu bringen. Man bezeichnet die Ordinalskala deshalb manchmal auch als Rangskala. Beispiele: Reihenfolge der besten Rennläufer, Schulnoten, oder die Mohs'sche Härteskala (bei der die Abstände nicht gleich sind).
- Intervallskala: Gleich unterteilte Einheiten entlang der Skala, ohne einen vordefinierten Nullpunkt. Beispiele: Temperatur (in C, F oder R), Wasserpegel eines Flusses. Intervallskalen können mit einer linearen Transformation vom Typ y = x+d transformiert werden ohne ihren Charakter zu verlieren (Intervallskalen bleiben also Intervallskalen, eventuell erreicht man dadurch sogar eine Verhältnisskala).
- Verhältnisskala: Gleich unterteilte Einheiten entlang einer Skala, mit einem wahren Nullpunkt. Beispiele: Temperatur in K, Gewicht, Geschwindigkeit. Verhältnisskalen können der Transformation y = k
 x+d unterzogen werden ohne ihren Typus zu verlieren. Diese Transformation entspricht zum Beispiel der Umrechnung von Metern in Zoll. x+d unterzogen werden ohne ihren Typus zu verlieren. Diese Transformation entspricht zum Beispiel der Umrechnung von Metern in Zoll.
Für verhältnisskalierte Daten gilt, dass ein doppelt so hoher Zahlenwert auch einem doppelt so hohen Eigenschaftswert entspricht (100 km/h ist doppelt so schnell wie 50 km/h). Im Gegensatz dazu gilt das für intervallskalierte Werte nicht (ein Pegelstand von 2.40 m ist nicht doppelt so hoch wie ein Pegel von 1.20 m, da der Nullpunkt ja willkürlich gewählt wurde; entsprechend bedeutet ein Pegelstand von null nicht einen exakt leeren Fluss).
Bitte beachten Sie, dass arithmetrische Verfahren nur für Intervall- und Verhältnisskalen sinnvoll sind. Multiplikation und Division sind nur auf Verhältnisskalen anwendbar. In vielen Bereichen der Statistik (z.B. in den Humanwissenschaften) sind Verhältnisskalen von geringer Bedeutung, da die meisten Messungen keinen wahren Nullpunkt aufweisen. Praktisch alle statistischen Verfahren die für intervallskalierte Daten entwickelt wurden, funktionieren auch mit verhältnisskalierten Daten. Man fasst deshalb die Intervall- und Verhältnisskalen unter dem Begriff metrische Skalen oder Kardinalskalen zusammen; nominal und ordinal skalierte Daten werden auch unter dem Begriff kategoriale Daten zusammengefasst.
Die folgende Tabelle fasst nochmals die Eigenschaften der verschiedenen Skalen zusammen und gibt ein paar Beispiele:
| Skalentyp |
mögliche Aussagen zu den Messwerten |
erlaubte Operatoren |
Beispiele |
| Nominalskala |
Gleichheit (bzw. Verschiedenheit), Abzählbarkeit |
=, 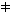 |
Farben, Telefonnummern, Gefühlslagen |
| Ordinalskala |
Gleichheit (bzw. Verschiedenheit), größer/kleiner-Relationen, Abzählbarkeit |
=, 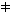 , <, > , <, > |
Bundesligatabelle, militärische Ränge, Energieeffizienzklassen, Schulnoten |
| Intervallskala |
Gleichheit (bzw. Verschiedenheit), größer/kleiner-Relationen, Gleichheit von Differenzen |
=, 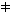 , <, >, +, - , <, >, +, - |
Jahreszahlen, Temperatur in Celsius, IQ-Skala |
| Verhältnisskala |
Gleichheit (bzw. Verschiedenheit), größer/kleiner-Relationen, Gleichheit von Differenzen, Gleichheit von Verhältnissen, Nullpunkt |
=, 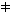 , <, >, +, -, *, / , <, >, +, -, *, / |
Geschwindigkeiten, Längen, Temperatur in Kelvin, Alter |
|


 Grundlagen
Grundlagen  Skalenniveau
Skalenniveau Grundlagen
Grundlagen  Skalenniveau
Skalenniveau

 x+d unterzogen werden ohne ihren Typus zu verlieren. Diese Transformation entspricht zum Beispiel der Umrechnung von Metern in Zoll.
x+d unterzogen werden ohne ihren Typus zu verlieren. Diese Transformation entspricht zum Beispiel der Umrechnung von Metern in Zoll.