| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Univariate Daten Univariate Daten  Verteilungen Verteilungen  z-Transformation z-Transformation |
|||
| Siehe auch: Skalenniveau, T-Scores, Dichotome Merkmale | |||
| Search the VIAS Library | Index | |||
|
z-TransformationAuthor: Hans Lohninger
Oft hat man das Problem, Stichprobenwerte vergleichbar zu machen, wobei es meist darauf ankommt, einzelne Werte einer Stichprobe in Bezug auf ihre Lage in der Stichprobenverteilung zu charakterisieren. Ein oft benütztes Hilfsmittel dazu ist die sogenannte z-Transformation, bei der die Werte einer Stichprobe in z-Werte (engl. z-scores) umgerechnet werden:
mit zi ... z-transformierte Stichprobenwerte Die z-Transformation wird auch als Standardisierung oder Autoskalierung bezeichnet. z-transformierte Werte werden vor allem dadurch vergleichbar, dass die Stichprobenwerte nach der Transformation nicht mehr in den Originalmaßeinheiten gemessen werden sondern in Vielfachen der Standardabweichung der Stichprobe. Außerdem ist der Mittelwert von z-Werten immer null. Falls die Originalwerte normalverteilt sind, sind die z-Werte standardnormalverteilt (μ=0, σ=1). Das folgende Beispiel zeigt den Effekt der Standardisierung von Daten. Nehmen wir an, wir hätten zwei Normalverteilungen, eine mit dem Mittelwert 10.0 und der Standardabweichung 30.0 (links oben), die andere mit einem Mittelwert von 200 und einer Standardabweichung von 20.0 (oben rechts). Die Standardisierung beider Datensätze ergibt nun vergleichbare Verteilungen, da die z-transformierten Verteilungen beide einen Mittelwert von 0.0 und eine Standardabweichung von 1.0 aufweisen (untere Zeile).
|
|||
Home  Univariate Daten Univariate Daten  Verteilungen Verteilungen  z-Transformation z-Transformation |
|||
Last Update: 2012-10-08


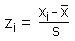
 ...
... 