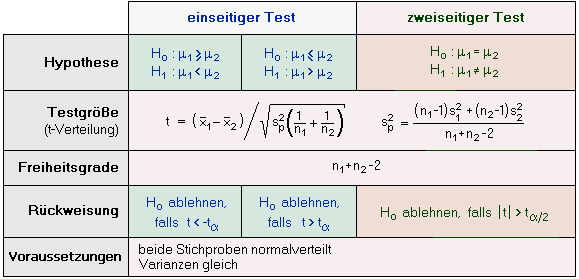| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Statistische Tests Statistische Tests  Mittelwerte Mittelwerte  Zweistichproben t-Test Zweistichproben t-Test  Zweistichproben-t-Test kleine Stichprobenmenge Zweistichproben-t-Test kleine Stichprobenmenge |
|||||
| Siehe auch: Zwei-Stichproben-t-Test - große Stichproben, Verteilungsrechner, Welch-Test | |||||
| Search the VIAS Library | Index | |||||
|
Zwei-Stichproben-t-Test - kleine StichprobenmengeAuthor: Hans Lohninger
Weil wir annehmen, dass σ12 und σ22 gleich sind, können wir eine gepoolte (zusammengelegte) Varianz sp2 (engl. pooled variance) berechnen. Die Zweckmäßigkeit für die Zusammenlegung der Varianzen liegt darin, eine bessere Schätzung der Varianz zu erhalten. Die gepoolte Varianz ist eine gewichtete Summe der Einzelvarianzen. Also ist, wenn n1 gleich n2 ist, sp2 nur der Durchschnitt der einzelnen Varianzen. Die Gesamtzahl der Freiheitsgrade ergibt sich aus der Summe der individuellen Freiheitsgrade der zwei Stichproben: df = df1 +df2 = (n1-1) + (n2-1) = n1+ n2 - 2 Um einen Zwei-Stichproben-t-Test einzusetzen, geht man nach folgendem Schema vor:
|
|||||
Home  Statistische Tests Statistische Tests  Mittelwerte Mittelwerte  Zweistichproben t-Test Zweistichproben t-Test  Zweistichproben-t-Test kleine Stichprobenmenge Zweistichproben-t-Test kleine Stichprobenmenge |
|||||
Last Update: 2021-08-15