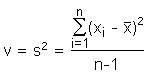Varianz

Author: Hans Lohninger

Zusätzlich zu den Lagemaßen, die man für die Beschreibung der Position der Verteilung einer Variablen braucht, muss man die Ausdehnung der Verteilung kennen und auch ihre Form. Klicken Sie das folgende interaktive Beispiel an, um einige Beispiele von gleichen Mittelwerten, aber verschiedenen Ausdehnungen zu sehen.

Die Ausdehnung einer Verteilung kann durch verschiedene Parameter beschrieben werden, von denen die Varianz die gebräuchlichste ist. Die Varianz v ist die Summe der quadrierten Abweichungen vom Mittelwert dividiert durch die Zahl der Proben minus 1:

Bei genauerer Betrachtung dieser Formel ergeben sich folgende Fragen:

• Warum wird die Quadratsumme und nicht etwa die Summe der absoluten Abweichungen vom Mittelwert zur Berechnung verwendet? Die Antwort: Die mathematische Analyse ist einfacher, wenn die Quadratsumme verwendet wird.
• Warum wird die Summe durch n-1 dividiert; wäre es nicht logischer, einfach n zu verwenden? Die Antwort ist nicht schwer, bedarf aber der Einführung des Konzepts der Freiheitsgrade.
• Was ist mit s² in der Formel? Die Antwort: Der Parameter s, der die Quadratwurzel der Varianz ist, wird Standardabweichung genannt.

Bitte beachten Sie bei der Bezeichnung für die Varianz und die Standardabweichung: Sie wird mit s² (bzw s) bezeichnet, wenn sie aus einer Stichprobe berechnet wurde. Wenn sie aus einer Grundgesamtheit berechnet wurde, wird die Standardabweichung durch den griechischen Buchstaben σ (Sigma) dargestellt.

Die Varianz mancher Daten ist eng verwandt mit der Präzision einer Messung. Betrachten Sie dazu das folgende interaktive Beispiel.