| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Mathematischer Hintergrund Mathematischer Hintergrund  Wahrscheinlichkeit Wahrscheinlichkeit  Additiv-Gesetz und einander ausschließende Ereignisse Additiv-Gesetz und einander ausschließende Ereignisse |
|||||
| Siehe auch: Summierung von Wahrscheinlichkeiten | |||||
| Search the VIAS Library | Index | |||||
|
Additiv-Gesetz - und einander ausschließende EreignisseAuthor: Administrator
Aus diesen Betrachtungen ergibt sich das Additiv-Gesetz für Vereinigungsmengen:
P(A) + P (B) = P(A also wird die Wahrscheinlichkeit der
Vereinigung zweier Ereignisse A und B durch:
P(A
erhalten.
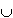 B) = P(A) + P (B) - P(A B) = P(A) + P (B) - P(A
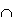 B). B).
Einander ausschließende Ereignisse:Die Ereignisse A und B sind einander ausschließende Ereignisse, wenn A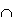 B keine Werte enthält, also
A und B keine Werte gemeinsam haben. In diesem Fall, ist die Wahrscheinlichkeit
der Vereinigung von einander ausschließenden Ereignissen einfach
die Summe ihrer Wahrscheinlichkeiten.
P(A B keine Werte enthält, also
A und B keine Werte gemeinsam haben. In diesem Fall, ist die Wahrscheinlichkeit
der Vereinigung von einander ausschließenden Ereignissen einfach
die Summe ihrer Wahrscheinlichkeiten.
P(A 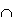 B) = P(A) + P(B) B) = P(A) + P(B)
|
|||||
Home  Mathematischer Hintergrund Mathematischer Hintergrund  Wahrscheinlichkeit Wahrscheinlichkeit  Additiv-Gesetz und einander ausschließende Ereignisse Additiv-Gesetz und einander ausschließende Ereignisse |
|||||
Last Update: 2012-10-08


 Die einfachste Methode die
Wahrscheinlichkeit einer Vereinigung von Ereignissen zu bestimmen, ist (bei
gleichen Einzelwahrscheinlichkeiten) die Abzählung der Elemente der
zusammengesetzten Menge. Dabei werden diejenigen Werte, die zu beiden
Ereignissen gehören, nur einmal gezählt. Wenn wir naiverweise aber versuchen die
Wahrscheinlichkeit der
Die einfachste Methode die
Wahrscheinlichkeit einer Vereinigung von Ereignissen zu bestimmen, ist (bei
gleichen Einzelwahrscheinlichkeiten) die Abzählung der Elemente der
zusammengesetzten Menge. Dabei werden diejenigen Werte, die zu beiden
Ereignissen gehören, nur einmal gezählt. Wenn wir naiverweise aber versuchen die
Wahrscheinlichkeit der