| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Mathematischer Hintergrund Mathematischer Hintergrund  Mengenlehre Mengenlehre  Vereinigungsmenge und Schnittmenge Vereinigungsmenge und Schnittmenge |
||||||||||||||||||||||||||||||||
| Siehe auch: Komplementärmenge und Untermenge, Summierung von Wahrscheinlichkeiten | ||||||||||||||||||||||||||||||||
| Search the VIAS Library | Index | ||||||||||||||||||||||||||||||||
|
Vereinigungsmenge und SchnittmengeAuthor: Administrator
Betrachtet man Ereignisse und die zugehörigen Wahrscheinlichkeiten, so findet man neben einfachen auch zusammengesetzte Ereignisse, die aus beliebig vielen Einzelereignissen bestehen können. Zusammengesetzte Ereignisse kann man als logische Kombination von einfachen Ereignissen betrachten, die man z.B. mit Venn-Diagrammen darstellen kann. Die einfachsten Kombinationen sind die Vereinigungsmenge und die Schnittmenge, die einem logischen ODER bzw. einem logischen UND entsprechen:
Beispiel: Betrachten wir das Spiel Roulette (die europäische Version mit einer Null): Wieviele Zahlen bringen einen Gewinn, wenn man auf rot
und die dritte Spalte setzt? Um das zu ermitteln müssen wir die
Vereinigungsmenge des Ereignisses A (die Zahl ist rot) und des Ereignisses B
(die Zahl steht in der dritten Spalte) bilden. A
Wieviele Zahlen gewinnen doppelt, wenn
man genau so setzt wie im vorigen Beispiel? Um bei beiden Wetten zu gewinnen,
müssen die Zahlen sowohl rot sein als auch in der rechten Spalte stehen. Die
Zahl der Gewinnzahlen kann man durch Ermittlung der Schnittmenge berechnen: A
Die Wahrscheinlichkeiten der jeweiligen zusammengesetzten Ereignisse lassen sich durch Abzählen und die Anwendung der Summenregel ermitteln. Für komplexere Aufgaben, bei denen ein Abzählen nicht mehr möglich ist kann man entsprechende Rechenregeln ableiten.
|
||||||||||||||||||||||||||||||||
Home  Mathematischer Hintergrund Mathematischer Hintergrund  Mengenlehre Mengenlehre  Vereinigungsmenge und Schnittmenge Vereinigungsmenge und Schnittmenge |
||||||||||||||||||||||||||||||||
Last Update: 2012-10-08


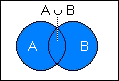 Als Vereinigungsmenge bezeichnet man die Menge aller Ereignisse die entweder zur Gruppe A gehören oder zur Gruppe B. Die Vereinigungsmenge entspricht dem logischen ODER und wird durch das Symbol
Als Vereinigungsmenge bezeichnet man die Menge aller Ereignisse die entweder zur Gruppe A gehören oder zur Gruppe B. Die Vereinigungsmenge entspricht dem logischen ODER und wird durch das Symbol 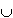 dargestellt.
dargestellt. Als Schnittmenge bezeichnet man die Menge aller Ereignisse, die sowohl zur Gruppe A als auch zur Gruppe B gehören. Die Schnittmenge entspricht dem logischen UND und wird durch das Symbol
Als Schnittmenge bezeichnet man die Menge aller Ereignisse, die sowohl zur Gruppe A als auch zur Gruppe B gehören. Die Schnittmenge entspricht dem logischen UND und wird durch das Symbol 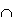 dargestellt.
dargestellt.