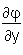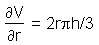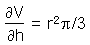| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Mathematischer Hintergrund Mathematischer Hintergrund  Diverses Diverses  Partielle Ableitung Partielle Ableitung |
|
| Siehe auch: Fehlerfortpflanzung, Literatur - Chemometrie | |
| Search the VIAS Library | Index | |
|
Partielle AbleitungAuthor: Hans Lohninger
Unter einer partiellen Ableitung versteht man die Ableitung einer Funktion mehrerer Variablen f(x1,...xn) bei der alle Variablen bis auf die abgeleitete konstant gehalten werden. Solche partielle Ableitungen haben einen vielfältigen Anwendungsbereich, von der Vektor-Algebra bis zur Differentialgeometrie.
Man schreibt eine partielle Ableitung mit dem Symbol
Beispiel:Betrachten wir einen Kegel, so wissen wir, dass das Volumen V des Kegels durch folgende Funktion bestimmt ist:V = V(r,h) = r2hπ/3. Nehmen wir an, dass wir die Höhe des Kegels konstant halten und nur dessen Radius ändern. Wenn wir die Änderung des Kegelvolumens in Abhängigkeit vom Radius wissen möchten, brauchen wir nur die partielle Ableitung nach r bilden:
|
|
Home  Mathematischer Hintergrund Mathematischer Hintergrund  Diverses Diverses  Partielle Ableitung Partielle Ableitung |
|
Last Update: 2021-08-15


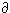 . Dieses Symbol ist gleich dem kursiven "d" der cyrillischen Schrift (eingeführt wurde das Symbol von Legendre). Möchte man ausdrücken, dass man eine Funktion φ nach einer bestimmten Variablen (z.B. y) partiell differenziert, so schreibt man das in folgender Form an:
. Dieses Symbol ist gleich dem kursiven "d" der cyrillischen Schrift (eingeführt wurde das Symbol von Legendre). Möchte man ausdrücken, dass man eine Funktion φ nach einer bestimmten Variablen (z.B. y) partiell differenziert, so schreibt man das in folgender Form an: