| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Univariate Daten Univariate Daten  Verteilungen Verteilungen  Wahrscheinlichkeits-Plot Wahrscheinlichkeits-Plot |
|||
| Siehe auch: QQ-Plot, Normalverteilung | |||
| Search the VIAS Library | Index | |||
|
Wahrscheinlichkeits-PlotAuthor: Hans Lohninger
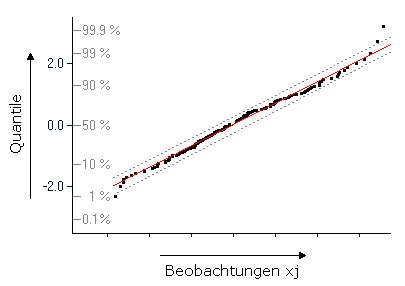
Eine Fragestellung, die immer wieder auftritt, ist die Frage, ob eine bestimmte Verteilung (z.B. die Normalverteilung) ein passendes Modell für die gemessenen Variablen darstellt. Dies ist insofern wichtig, da viele Verfahren bestimmte Annahmen bezüglich der Verteilungsform machen. Außerdem kann man aus der Verteilungsform eventuell auf bestimmte Eigenschaften des betrachteten Prozesses schließen. So kann man z.B. schließen, dass die Ausfallsrate konstant ist, falls die Zeiten bis zum Ausfall eines Produkts exponentiell verteilt sind. Eines der am häufigsten eingesetzen Werkzeuge zur visuellen Erkennung einer bestimmten Verteilungsform sind Histogramme. Allerdings benötigt man für Histogramme ein große Menge an Beobachtungen, um die Verteilungsform erkennen zu können, bei kleineren Stichprobengrößen kommt überdies noch der Effekt der Klassengrenzen dazu, der zu falschen Schlussfolgerungen führen kann. Daher wurde schon sehr früh sog. "Wahrscheinlichkeitspapier" entwickelt, das es auf einfache Weise erlaubt auf eine bestimmte Verteilung (meist die Normalverteilung) zu prüfen. Eine moderne Form des Wahrscheinlichkeitspapiers sind die Wahrscheinlichkeits-Plots. Zur Erstellung eines Wahrscheinlichkeits-Plots werden die Beobachtungen zuerst aufsteigend sortiert und die Beobachtungen x1, x2, ..., xj, ... xn bekommen entsprechend der sortierten Reihenfolge Rangzahlen j (im Bereich 1 bis n) zugewiesen. Die geordneten Beobachtungen werden nun gegen die Quantile der kumulierte Häufigkeit (j-0.5)/n aufgetragen. Die Quantile sind aus der Verteilung zu berechnen, auf die die Daten geprüft werden sollen.
Liegen die Daten in diesem Plot ungefähr auf einer Geraden, so nimmt man an, dass die gewählte Verteilung die Daten korrekt wieder gibt. Wie weit die einzelnen Datenpunkte von der Geraden abweichen dürfen, ist sicherlich subjektiv und hängt auch von der Zahl der Beobachtungen ab. In der Praxis sollte man für die Entscheidung ob die Daten der überprüften Verteilung entstammen, die Punkte am Rand weniger stark beachten als die mittleren 90% der Daten.
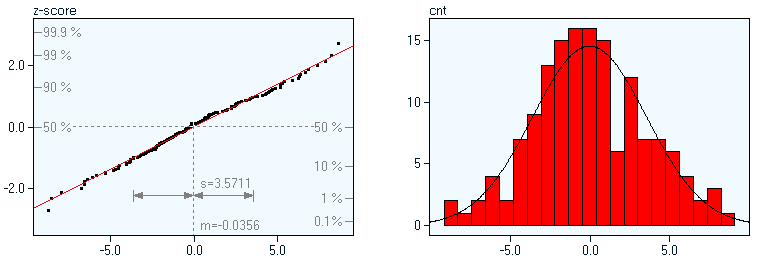
Die folgenden Beispiele zeigen Stichproben von 150 Beobachtungen aus verschiedenen Verteilungen, links jeweils der Wahrscheinlichkeits-Plot für die Normalverteilung, rechts das zugehörige Histogramm. Normalverteilung (Schiefe: 0.111): die Werte im Wahrscheinlichkeits-Plot liegen entlang einer Geraden
rechtsschiefe Verteilung (Schiefe: 0.870): die Werte im Wahrscheinlichkeits-Plot liegen auf einer nach unten gekrümmten Kurve
linksschiefe Verteilung (Schiefe: -1.363): der Wahrscheinlichkeits-Plot zeigt eine nach oben gewölbte Kurve
|
|||
Home  Univariate Daten Univariate Daten  Verteilungen Verteilungen  Wahrscheinlichkeits-Plot Wahrscheinlichkeits-Plot |
|||
Last Update: 2012-10-08