| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Statistische Tests Statistische Tests  Mittelwerte Mittelwerte  U-Test nach Wilcoxon, Mann und Whitney U-Test nach Wilcoxon, Mann und Whitney |
|||||||
| Siehe auch: Wilcoxon-Vorzeichen-Rangtest für Paardifferenzen, Differenzen-t-Test | |||||||
| Search the VIAS Library | Index | |||||||
|
U-Test nach Wilcoxon, Mann und WhitneyAuthor: Administrator
Manchmal kommt es bei t-Tests zum Vergleich von Mittelwerten (genauer formuliert beim t-Test für Mittelwertsdifferenzen) zu Ergebnissen, denen man nicht so richtig traut. In diesem Fall eignet sich die Kontrolle mit dem U-Test nach Wilcoxon, Mann und Whitney.(1) Dieser Test ist auch dafür geeignet im Falle nicht-normaler Verteilungen der Werte, auf die Gleichheit der Mittelwerte zu testen. Als einzige Voraussetzung gilt die Bedingung, dass die Form der Verteilungen der beiden zu vergleichenden Stichproben gleich ist (und genau genommen stetig sein müssen).(2) Der U-Test prüft folgende Nullhypothese: Die Wahrscheinlichkeit einer Beobachtung aus den beiden Grundgesamtheiten ist für jede der beiden Grundgesamtheiten gleich (d.h. die Verteilungen sind gleich):
H0: F1(x) = F2(x) für alle x Das Prinzip des U-Tests basiert auf folgender Überlegung: Sortiert man die Messwerte der beiden Stichproben in einer gemeinsamen Liste in aufsteigender Reihenfolge, so werden die Rangsummen der beiden Stichproben sich nur dann unterscheiden, wenn im Durchschnitt die beiden Stichproben sich unterscheiden (also die eine Stichprobe im Durchschnitt kleinere Werte aufweist als die andere). Zur Berechnung der Prüfgröße U werden die Stichproben gemeinsam sortiert und jeweils notiert welcher Messwert zu welcher Stichprobe gehört. Die Summe der Rangzahlen für die Stichprobe 1 sei R1, die für die Stichprobe 2, R2. Dann gilt für die Testgröße U:
U1 = n1*n2 + n1(n1+1)/2 - R1 Die gesuchte Prüfgröße U ist die kleinere von U1 und U2: U = min (U1, U2)
Die Nullhypothese H0 wird verworfen, wenn der berechnete U-Wert kleiner oder gleich dem kritischen Wert Ukrit(n1, n2, α). Das Verwerfen der Nullhypothese bedeutet, dass die Verteilungen nicht gleich sind. Da man aber als Voraussetzung gleiche Verteilungsformen annimmt, folgt daraus, dass die Mittelwerte ungleich sein müssen, falls die Nullhypothese abgelehnt wird.
|
|||||||
Home  Statistische Tests Statistische Tests  Mittelwerte Mittelwerte  U-Test nach Wilcoxon, Mann und Whitney U-Test nach Wilcoxon, Mann und Whitney |
|||||||
Last Update: 2012-12-09


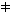 F2(x) für mindestens ein x
F2(x) für mindestens ein x