| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Statistische Tests Statistische Tests  Mittelwerte Mittelwerte  Gepaarte Experimente Gepaarte Experimente |
|||||
| Siehe auch: Testen von Hypothesen, Verteilungsrechner, Wilcoxon-Vorzeichen-Rangtest für Paardifferenzen, U-Test nach Wilcoxon, Mann und Whitney, Voraussetzung von statistischen Tests | |||||
| Search the VIAS Library | Index | |||||
|
Differenzen-t-TestAuthor: Hans Lohninger
Voraussetzung für den Differenzen-t-Test: Die Verteilung der Differenzen ist normal(1) und die Differenzen sind intervallskaliert. Das gepaarte Differenzenexperiment ist oft mächtiger, da es Unterschiede in den Stichproben eliminieren kann, die die Gesamtvarianz σ2 anheben. Wenn Vergleiche zwischen Gruppen gemacht werden (mit ähnlichen experimentellen Einheiten), wird dies Blockbildung (engl. blocking) genannt. Das gepaarte Differenzenexperiment ist ein einfaches Beispiel eines randomisierten geblockten Experiments. Ist die Normalverteilungsannahme für die Differenzen nicht erfüllt, kann der nicht-parametrische Wilcoxon-Rangsummentest für Versuchspläne mit gepaarten Differenzen verwendet werden.
|
|||||
Home  Statistische Tests Statistische Tests  Mittelwerte Mittelwerte  Gepaarte Experimente Gepaarte Experimente |
|||||
Last Update: 2014-04-28


 Beim Vergleich von Methoden und Verfahren, bei denen Daten verwendet werdem, die aus derselben
Beim Vergleich von Methoden und Verfahren, bei denen Daten verwendet werdem, die aus derselben 
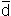 bzw. sd; nD ist die Anzahl der Paare. Abhängig von der Stichprobengröße nD wenden wir den Ein-Stichprobentest basierend auf
bzw. sd; nD ist die Anzahl der Paare. Abhängig von der Stichprobengröße nD wenden wir den Ein-Stichprobentest basierend auf 