Ausreißertest nach Walsh

Author: Hans Lohninger

J.E. Walsh entwickelte einen nicht-parametrischen Test, um Ausreißer in einem beliebigen Datensatz zu detektieren. Dieser Test erfordert zwar eine große Zahl an Beobachtungen (n > 220 für ein Signifikanzniveau von α = 0.05), kann dafür aber für nicht-normalverteilte Daten angewendet werden. Die folgenden Anweisungen beschreiben die Durchführung des Walsh-Tests für große Stichproben:

Nehmen wir an, dass X₁, X₂, ... , X_n die Folge der in aufsteigender Reihenfolge sortierten Daten repräsentiert. Falls n<60 ist, darf der Test nicht durchgeführt werdem, falls 60<n<=220, dann liegt das Signifikanzniveau α bei 0.10, bei größerem n (n >220) liegt es bei 0.05.

Schritt 1:	Zuerst definiert man die Zahl der möglichen Ausreißer r >= 1.
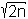Schritt 2:	Dann berechnet man c = ceil(), k = r + c, b2 = 1/α, und wobei ceil() die Rundung zur nächst-größeren ganzen Zahl bezeichnet (Beispiel: aus 3.21 wird 4).
Schritt 3:	Die r kleinsten Punkte sind Ausreißer (bei einem Signifikanzniveau α), falls Xr - (1+a)Xr+1 + aXk < 0 gilt
Schritt 4:	Die r größten Punkte sind Ausreißer (bei einem Sigifikanzniveau α), falls Xn+1-r - (1+a)Xn-r + aXn+1-k > 0 gilt.
Schritt 5:	Falls beide Ungleichungen erfüllt sind, sind sowohl die kleinen als auch die großen Werte als Ausreißer anzusehen.