| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Statistische Tests Statistische Tests  Ausreissertests Ausreissertests  Nalimov-Test Nalimov-Test |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Siehe auch: Dean-Dixon Ausreißertest | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Search the VIAS Library | Index | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Nalimov-TestAuthor: Hans Lohninger
Unter der Annahme, dass eine Normalverteilung vorliegt, kann man folgenden einfachen Test auf Ausreißer durchführen (dieser Test wird in der deutschsprachigen Literatur manchmal auch Nalimov-Test (1) genannt). Demnach liegt bei einem Wert x1 ein Ausreißer vor, wenn die Testgröße q
die kritische Grenze qcrit für ein gegegebenes Signifikanzniveau überschreitet. Die Zahl der Freiheitsgrade f ergibt sich aus f = n-2 (Tabelle nach Kaiser/Gottschalk
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Home  Statistische Tests Statistische Tests  Ausreissertests Ausreissertests  Nalimov-Test Nalimov-Test |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Last Update: 2012-10-08


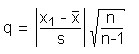
 ....
....