| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Multivariate Data Multivariate Data  Modeling Modeling  Neural Networks Neural Networks  Extrapolation Extrapolation |
|||
| See also: Generalization and Overtraining, Extrapolation | |||
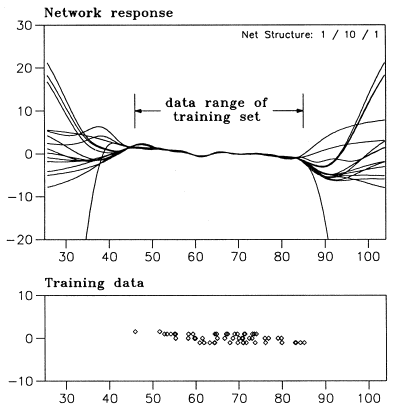
Neural Networks - ExtrapolationNeural networks exhibit a major drawback when compared to linear methods
of function approximation: they cannot extrapolate. This is due to the
fact that a neural network can map virtually any function by adjusting
its parameters according to the presented training data. For regions of
the variable space where no training data is available, the output of a
neural network is not reliable.
Basically, the data space which can be processed by a trained neural network is split into two regions:
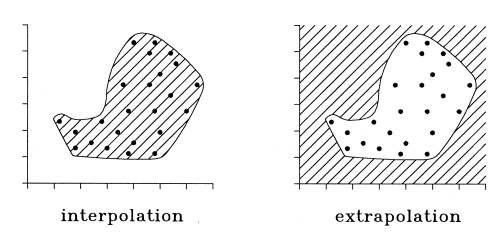
In order to overcome this problem, one should in some form record the
range of the variable space where training data is available. In principle,
this could be done by calculating the convex hull of the training data
set. If unknown data presented to the net are within this hull, the output
of the net can be considered as reliable. However, the concept of the convex
hull is not satisfactory since this hull is complicated to calculate and
provides no solution for problems where the input data space is concave.
A better method, proposed by Leonard et al.
|
|||
Home  Multivariate Data Multivariate Data  Modeling Modeling  Neural Networks Neural Networks  Extrapolation Extrapolation |
|||