| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Statistical Tests Statistical Tests  ANOVA ANOVA  ANOVA - How to perform it ANOVA - How to perform it |
|||||||||||||||
| See also: ANOVA, Combination of Several Distributions | |||||||||||||||
ANOVA - How to perform itWhen performing an ANOVA the following basic assumptions have to be met
If these assumptions are not met, the analysis of variance can still be performed, but using different test procedures which are beyond the scope of this text.
Assuming that the data follows a normal distribution, we first have to test for equal variances(1). Depending on the samples several tests are available:
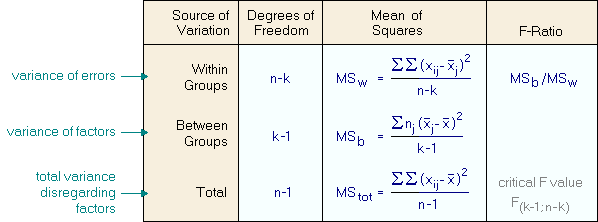
In the next step the analysis of variances is performed (remember the goal is to compare means, not variances). The null hypothesis for the ANOVA is that all sample means are the same. In order to achieve the ANOVA we have to calculate the mean of squares(2) within each sample MSw and the mean of squares among the samples MSb. The mean of squares (MS) is defined as the sum of squares divided by the degrees of freedom. The test statistic F, which is defined by the ratio of MSb to MSw, is distributed according to an F distribution. A value higher than the critical value Fk-1;n-k indicates that the null hypothesis has to be rejected.
|
|||||||||||||||
Home  Statistical Tests Statistical Tests  ANOVA ANOVA  ANOVA - How to perform it ANOVA - How to perform it |
|||||||||||||||