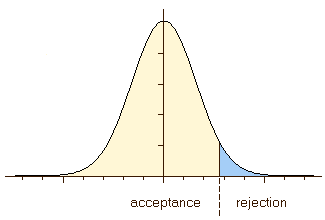
One-Sided vs. Two-Sided Tests

Since making a decision is - statistically speaking - the selection of a threshold value on a one-dimensional scale (i.e. on the argument axis of the probability density plot), we have to distinguish between two cases: first, one may ask whether a property lies above or below a pre-defined threshold (left figure, below). In this case we have to apply a one-sided test. Secondly, one may be interested to determine whether a property is within certain boundaries. This question involves setting two boundaries and asks for the probability of an event lying either between or outside these boundaries (right figure). In this case we have to apply a two-sided test.

Example:

Does the iron concentration of an iron ore exceed 30 %? [one sided test]
Is the pizza you ordered from the pizza service well done (it could be raw, or burnt, or well done) [two sided test]

Generally speaking, we base the decision on the value of a test statistic, e.g. the average concentration of iron or the degree of "done-ness" of the pizza. This test statistic can be an average of a property, its variance etc. The set of all possible values of this test statistic is called the sample space. Our decision divides the sample space into two mutually exclusive regions: the acceptance region and the rejection region. When you look at the figure above, it immediately becomes clear why some tests are called one-sided and others are called two-sided. One-sided tests have one rejection region, i.e. you check whether the parameter of interest is larger (or smaller) than a given value. Two-sided tests are used when we test a parameter for equivalence to a certain value. Deviations from that value in both directions are rejected.