Uncorrelated Residuals - Durbin-Watson Test

One of the prerequisites for linear regression is that the residuals must not be serially correlated. A possible serial correlation of the residuals indicates that the selected regression model does not fully explain the actual relationship. If the residuals are ordered due to an inherently ordered independent variable as this occurs, for example, in time series, we speak of an autocorrelation of the residuals.

The correlation of the residuals may lead to one of the following problems:

• The calculated standard errors of the regression coefficients may be significantly smaller than they actually are. This in effect pretends a higher precision of the calculated model.
• As a consequence of smaller estimated standard errors, the confidence intervals and the levels of significance of the parameters are becoming invalid.

Although the correlation structure of the residuals may be arbitrarily complex, the most common and simplest case (i.e. the serial correlation of neighboring data values) is easy to check for. The most popular test for serial correlation is the Durbin-Watson test.

This test is based on the assumption that consecutive residuals ε are correlated according to the following equation:

ε_t = ρε_t-1 + ω_t,

with |ρ| < 1.

ρ is the correlation of the residuals, the weight ω is normally distributed having a mean of 0 and a constant variance.

The null hypothesis of the Durbin-Watson test assumes the correlation to be zero:

H₀ : ρ = 0
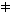H₁ : ρ 0