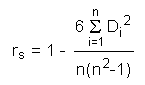Rangkorrelation nach Spearman

Author: Hans Lohninger

Für die Berechnung des Pearson'schen Korrelationskoeffizienten müssen die beiden betrachteten Variablen intervallskaliert sein und der Zusammenhang zwischen den beiden Variablen wird als linear angenommen. Im Fall von nicht-linearen Zusammenhängen, und/oder ordinalen Variablen führt der Korrelationskoeffizient nach Pearson zu falschen Ergebnissen. Eine Lösung für diese Situation kann die Verwendung des Spearman'schen Rangkorrelationskoeffizienten r_s sein. Für diesen ist kein linearer Zusammenhang vorausgesetzt, der Zusammenhang muss lediglich monoton sein. Der Korrelationskoeffizient nach Spearman kann auch auf ordinale Werte angewendet werden.

Grundsätzlich unterscheidet sich r_s von der Korrelation nach Pearson nur darin, dass die Werte zu Rängen umgeformt werden, bevor der Korrelationskoeffizient berechnet wird. Die numerische Äquivalenz gilt nur falls keine Bindungen (gleiche Werte mehrfach) auftreten, andernfalls wird sich der Spearman'sche Koeffizient vom Pearson'schen Koeffizienten unterscheiden.

Wenn man die Beobachtungen durch die entsprechenden Rangzahlen ersetzt, kann die Gleichung für den Korrelationskoeffizienten vereinfacht werden. Daraus ergibt sich folgende Formel:

mit D_i als Differenzen der Rangzahlen. Die Gleichung ist gültig, wenn n größer als 4 ist. Im Fall von Bindungen muss man den arithmetischen Mittelwert der korrespondierenden Rangzahlen nehmen.

Beispiel:

Zwei Personen verkosten 10 italienische Rotweine und bewerten sie mit einer ordinalen Notenskala von 1 bis 5. Die Ergebnisse der Bewertung sind wie folgt: Noten Noten Wein Nr. Person 1 Person 2 1 1 2 2 2 3 3 4 5 4 5 4 5 2 2 6 2 2 7 4 3 8 3 4 9 1 3 10 4 2 Um den Spearman'schen Rangkorrelationskoeffizienten zu berechnen müssen wir zuerst die Noten für jede Person sortieren. Falls mehrere Proben dieselbe Note bekommen haben, werden die Rangzahlen gemittelt: Noten Rang Rang Wein Nr. Person 1 (Bindungen) 1 1 1 1.5 9 1 2 1.5 6 2 3 4 5 2 4 4 2 2 5 4 8 3 6 6 10 4 7 8 7 4 8 8 3 4 9 8 4 5 10 10 Noten Rang Rang Wein Nr. Person 2 (Bindungen) 5 2 1 2.5 1 2 2 2.5 10 2 3 2.5 6 2 4 2.5 2 3 5 6 7 3 6 6 9 3 7 6 8 4 8 8.5 4 4 9 8.5 3 5 10 10 Die fertige Rangtabelle inkludiert auch die Differenzen der Ränge und die quadrierten Differenzen: Wine Nr. Person 1 Rang Person 2 Rang Rang quadrierte Differenz Diff. 1 1 1.5 2 2.5 -1 1 2 2 4 3 6 -2 4 3 4 8 5 10 -2 4 4 5 10 4 8.5 1.5 2.25 5 2 4 2 2.5 1.5 2.25 6 2 4 2 2.5 1.5 2.25 7 4 8 3 6 2 4 8 3 6 4 8.5 -2.5 6.25 9 1 1.5 3 6 -4.5 20.25 10 4 8 2 2.5 5.5 30.25 ------------------------------------------------------------------------ Summe 0.0 76.50 Die Summe der quadrierten Differenzen wird nun zur Berechnung des Spearman'schen Rangkorrelationskoeffizient verwendet: rs = 1 - (6*76.5/(10*(100-1)) = 0.5364