| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Statistische Tests Statistische Tests  Mittelwerte Mittelwerte  Einstichproben t-Test Einstichproben t-Test  Einstichproben-t-Test große Stichproben Einstichproben-t-Test große Stichproben |
|
| Siehe auch: Ein-Stichproben-t-Test - kleine Stichproben, Zwei-Stichproben-t-Test, Verteilungsrechner, Ein-Stichproben-t-Test | |
| Search the VIAS Library | Index | |
|
Einstichproben-t-Test - große StichprobenAuthor: Hans Lohninger
Die Entscheidung kann anhand der Tabelle getroffen werden:
1. Wir müssen zwei Hypothese formulieren (die Nullhypothese H0 und die Alternativhypothese H1): H0: Menge <= Limit 2. Als Nächstes bestimmen wir das Signifikanzniveau, das unseren Ansprüchen entspricht (ein übliches Signifikanzniveau ist 5 %). 3. Um zu entscheiden, welche der zwei Hypothesen zutrifft, berechnen wir die Testgröße
die normal verteilt ist. Der z-Wert gibt uns den Abstand des
gemessenen
4. Nun legen wir den Bereich der Ablehnung fest. Um zu wissen, wann die
Nullhypothese verworfen werden muss (d.h.
5. Zum Schluss müssen wir die geeignete Hypothese auswählen, indem wir die numerischen Werte für 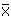 , μ, σ und n in die Gleichung für z einsetzen. Wir verwerfen die
Nullhypothese nicht (beachten Sie den feinen Unterschied zu "wir nehmen die
Nullhypothese an"), wenn der errechnete z-Wert kleiner als zx = 1,645
ist. , μ, σ und n in die Gleichung für z einsetzen. Wir verwerfen die
Nullhypothese nicht (beachten Sie den feinen Unterschied zu "wir nehmen die
Nullhypothese an"), wenn der errechnete z-Wert kleiner als zx = 1,645
ist.
Anmerkung: Ein allgemeinerer Ansatz ist, die t-Verteilung zu verwenden, da sich diese bei großen Stichproben ohnehin der Normalverteilung annähert.
|
|
Home  Statistische Tests Statistische Tests  Mittelwerte Mittelwerte  Einstichproben t-Test Einstichproben t-Test  Einstichproben-t-Test große Stichproben Einstichproben-t-Test große Stichproben |
|
Last Update: 2012-10-08


 Lassen Sie uns davon ausgehen, dass wir Behälter mit einer
teuren Substanz füllen müssen. Unser Kunde erwartet eine garantierte Menge μ des bestellten Materials. Wir kennen die Genauigkeit σ der Maschine und wollen prüfen, ob die Abfüllanlage
richtig eingestellt ist. Da die Messungen recht kostengünstig sind (d.h.
wir müssen nur den Behälter wiegen), können wir uns eine große Zahl von
Messungen leisten. Dabei stellt sich folgende Frage: Wie groß muss die
durchschnittliche Füllmenge sein, dass wir die Annahme, der Füllvorgang verläuft
richtig, nicht verwerfen müssen? Da wir die Möglichkeit einer falschen
Entscheidung eingestehen müssen, sind wir zufrieden, wenn die
Fehlerwahrscheinlichkeit kleiner als α% ist. Die
Wahrscheinlichkeit α wird als Signifikanzniveau
bezeichnet.
Lassen Sie uns davon ausgehen, dass wir Behälter mit einer
teuren Substanz füllen müssen. Unser Kunde erwartet eine garantierte Menge μ des bestellten Materials. Wir kennen die Genauigkeit σ der Maschine und wollen prüfen, ob die Abfüllanlage
richtig eingestellt ist. Da die Messungen recht kostengünstig sind (d.h.
wir müssen nur den Behälter wiegen), können wir uns eine große Zahl von
Messungen leisten. Dabei stellt sich folgende Frage: Wie groß muss die
durchschnittliche Füllmenge sein, dass wir die Annahme, der Füllvorgang verläuft
richtig, nicht verwerfen müssen? Da wir die Möglichkeit einer falschen
Entscheidung eingestehen müssen, sind wir zufrieden, wenn die
Fehlerwahrscheinlichkeit kleiner als α% ist. Die
Wahrscheinlichkeit α wird als Signifikanzniveau
bezeichnet.

 ,
,