Test: Korrelationskoeffizient

Author: Hans Lohninger

Ein Korrelationskoeffizient von null zeigt an, dass es keine lineare Beziehung zwischen zwei Variablen gibt. Um die Signifikanz eines Korrelationskoeffizienten zu testen, können wir eine t-Statistik verwenden:

Diese Teststatistik folgt einer t-Verteilung. Vom Korrelationskoeffizienten wird angenommen, dass er statistisch signifikant ist, wenn der berechnete Wert größer als der kritische Wert einer t-Verteilung mit einem Signifikanzniveau von α/2 und n-2 Freiheitsgraden ist.

Um nun die Hypothese zu testen, ob sich ein berechneter Korrelationskoeffizient r von dem Populationskoeffizienten ρ unterscheidet, müssen wir die Testgröße z, die eine Standardnormalverteilung aufweist, berechnen. Von r und ρ wird angenommen, dass sie nicht von derselben Population stammen, wenn z größer als der kritische Wert einer Standardnormalverteilung mit einem ausgewählten Signifikanzniveau ist.

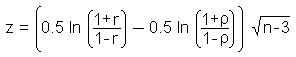(Für negative Werte von r oder ρ müssen die Absolutwerte verwendet werden.)