| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Statistische Tests Statistische Tests  Verteilungen Verteilungen  Shapiro-Wilk-Test Shapiro-Wilk-Test |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Siehe auch: Test auf Normalverteilung | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Search the VIAS Library | Index | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Shapiro-Wilk-TestAuthor: Hans Lohninger
Der Shapiro-Wilk-Test Die grundlegende Idee des Shapiro-Wilk-Tests besteht darin, dass man die Varianz auf zwei Arten schätzt: zum einen durch eine Regression im QQ-Plot und zum anderen durch die Stichprobenvarianz. Die beiden Schätzungen sollten für eine Normalverteilung nahe beieinander liegen und damit den Quotienten 1 ergeben. Zu kleine Werte des Quotienten führen zu einer Ablehnung der Normalverteilungshypothese.
Zur Berechnung der Testgröße W geht man wie folgt vor:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Home  Statistische Tests Statistische Tests  Verteilungen Verteilungen  Shapiro-Wilk-Test Shapiro-Wilk-Test |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Last Update: 2012-10-08



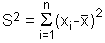
 , mit k = n/2.
, mit k = n/2. 