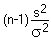| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Univariate Daten Univariate Daten  Verteilungen Verteilungen  Prüfverteilungen Prüfverteilungen  Chi-Quadrat-Verteilung Chi-Quadrat-Verteilung |
|
| Siehe auch: Stichprobenverteilungen, t-Verteilung, F-Verteilung, Ein-Stichproben Chi-Quadrat-Test | |
| Search the VIAS Library | Index | |
|
Chi-Quadrat-VerteilungAuthor: Hans Lohninger
Um Rückschlüsse über die Verteilung der Grundgesamtheit auf der Basis der Probenvarianz zu ziehen, müssen wir eine spezielle Verteilung berücksichtigen, die Chi-Quadrat-Verteilung (χ2): Ist eine zufällige Variable Y normal verteilt (mit dem Mittelwert µ und der Varianz σ2), dann zeigt die Größe
eine χ2-Verteilung mit n-1 Freiheitsgraden für eine zufällige Stichprobe der Größe n. Einige Beispiele für die χ2-Verteilung für verschiedene Freiheitsgrade werden in der Darstellung unten gezeigt.
Wie Sie sehen können, ist die χ2-Verteilung asymmetrisch und immer positiv. Der Mittelwert der χ2-Verteilung ist gleich der Anzahl der Freiheitsgrade n-1; die Varianz ist gleich der doppelten Anzahl an Freiheitsgraden. Die χ2-Verteilung ist in statistischen Tabellen aufgelistet oder kann online mit Hilfe des Verteilungsrechners berechnet werden. Die χ2-Verteilung wird zum Testen der Unterschiede zwischen Grundgesamtheiten und Probenvarianzen sowie zwischen theoretischen und beobachteten Verteilungen verwendet. Eine wichtige Eigenschaft der χ2-Verteilung ist deren Additivität: Wenn zwei unabhängige Größen χ2-verteilt sind (mit den Freiheitsgraden f1 und f2), dann ist die Summe der beiden Größen χ2-verteilt mit dem Freiheitsgrad f1+f2.
|
|
Home  Univariate Daten Univariate Daten  Verteilungen Verteilungen  Prüfverteilungen Prüfverteilungen  Chi-Quadrat-Verteilung Chi-Quadrat-Verteilung |
|
Last Update: 2012-10-08