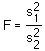| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Univariate Daten Univariate Daten  Verteilungen Verteilungen  Prüfverteilungen Prüfverteilungen  F-Verteilung F-Verteilung |
|||||||
| Siehe auch: Stichprobenverteilungen, Chi-Quadrat-Verteilung, t-Verteilung, Zwei-Stichproben-F-Test | |||||||
| Search the VIAS Library | Index | |||||||
|
F-VerteilungAuthor: Hans Lohninger
Die F-Verteilung (nach R.A. Fisher benannt) ist relevant für die Berechnung der Verhältnisse der Varianzen von normal verteilten Statistiken. Nehmen wir an, wir haben zwei Stichproben mit n1 und n2 Beobachtungen. Das Verhältnis
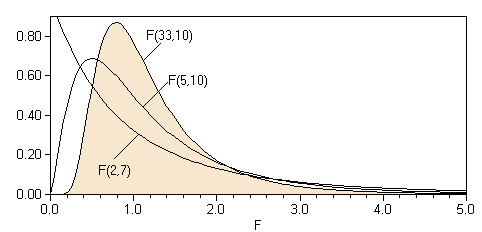
ist nach einer F-Verteilung verteilt, mit df1 = n1-1 Freiheitsgraden für den Zähler des Quotienten und mit df2 = n2-1 Freiheitsgraden für den Nenner. Die F-Verteilung ist nach rechts verschoben und die F-Werte können nur positiv sein.
Beachten Sie, dass drei der wichtigsten Verteilungen (nämlich die
Normalverteilung, die t-Verteilung und die Chi-Quadrat-Verteilung) als
Spezialfälle der F-Verteilung angesehen werden können:
|
|||||||
Home  Univariate Daten Univariate Daten  Verteilungen Verteilungen  Prüfverteilungen Prüfverteilungen  F-Verteilung F-Verteilung |
|||||||
Last Update: 2012-10-18