| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Allgemeine Bearbeitungsschritte Allgemeine Bearbeitungsschritte  Datenvorverarbeitung Datenvorverarbeitung  Transformation von Daten-Räumen Transformation von Daten-Räumen  Beispiel: Massenspektrometrie Beispiel: Massenspektrometrie |
|
| Siehe auch: ANN - Einführung, Autokorrelation, Transformation von Datenräumen | |
| Search the VIAS Library | Index | |
|
Transformation von Datenräumen - Beispiel: MassenspektrometrieAuthor: Hans Lohninger
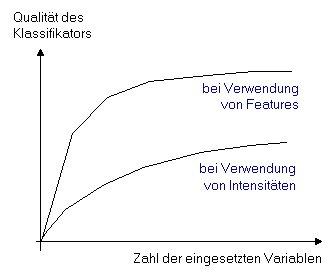
Ein Beispiel für die erfolgreiche Transformation eines Datenraums kommt aus der Massenspektrometrie. Obwohl dieses Beispiel sehr speziell und möglicherweise für Lernende ohne Hintergrundwissen zur Chemie und Physik schwer zu verstehen ist, zeigt es doch deutlich die Vorteile der Einführung von Wissen in einen Modellierungsprozess. Eine bekannte Eigenschaft von Massenspektren (MS) von Alkyl-Verbindungen ist das Auftreten von regelmäßig angeordneten Peak-Gruppen mit einem Unterschied von 14 Masseneinheiten. Diese periodischen Peaks ergeben sich, weil Alkyl-Ketten an jeder Kohlenstoff-Kohlenstoff-Bindung mit ungefähr derselben Wahrscheinlichkeit brechen; deshalb werden Fragmente erzeugt, die sich in der Masse durch ein ganzzahliges Vielfaches der CH2-Gruppen (m/e = 14) unterscheiden. Substanzen, die keine Alkyl-Gruppen enthalten, zeigen diese Periodizität in ihren Massenspektren natürlich nicht. Diese Eigenschaft kann nun dazu verwendet werden, einen Klassifikator für die Unterscheidung zwischen Alkyl- und Nicht-Alkyl-Verbindungen zu erzeugen. Wir können nun versuchen, in einer ersten, etwas naiven Vorgehensweise ein neuronales Netzwerk darauf zu trainieren, diese Periodizitäten in den Massenspektren zu entdecken. Aber Periodizitäten zu entdecken, ist teilweise schwer für neuronale Netzwerke (wie für jede andere Methode). Also benötigt man ein relativ großes Netzwerk, um diese Aufgabe zu erfüllen - mit all den Nachteilen eines großen Netzwerks (z.B. Overfitting). Auch ist der Eingangsvektor des Netzwerks relativ groß (das gesamte Massenspektrum typischerweise mehrere hundert Elemente pro Vektor), was den Trainingsprozess beträchtlich verlangsamt. Nun wollen wir unser Wissen über das Fragmentierungsverhalten von Alkyl-Verbindungen mit einbringen. Weil wir wissen, dass Alkyl-Verbindungen periodische Massenspektren liefern, transformieren wir den Originaldatenraum (den MS-Vektor) zu einer einzigen Variablen, die die periodischen Peaks in den Massenspektren widerspiegelt. Dazu berechnen wir den Wert der Autokorrelationsfunktion mit einer Verschiebung von 14. Dieser Wert wird für die Massenspektren, die periodische Peaks mit einem Abstand von 14 Massen zeigen, hoch sein, und für alle anderen Spektren niedrig. Nun kann das Problem leicht gelöst werden, indem man einen nur eindimensionalen Eingang und ein vergleichsweise kleines ANN verwendet. Natürlich kann dieses Konzept erweitert und so auf Daten angewendet werden, dass unser gesamtes Wissen in solchen neuen Variablen verschlüsselt ist. Indem man das tut, wird der originale n-dimensionale Datenraum (im Fall der Massenspektrometrie kann n leicht 500 übersteigen) zu einem p-dimensionalen Raum transformiert, wobei p üblicherweise um vieles kleiner als n ist. Die Darstellung unten zeigt den Effekt der Anwendung von Deskriptoren, die auf Wissen basieren, im Vergleich zu Originaldaten. Die Klassifikationsaufgabe kann durch die Verwendung solcher Deskriptoren viel besser gelöst werden.
|
|
Home  Allgemeine Bearbeitungsschritte Allgemeine Bearbeitungsschritte  Datenvorverarbeitung Datenvorverarbeitung  Transformation von Daten-Räumen Transformation von Daten-Räumen  Beispiel: Massenspektrometrie Beispiel: Massenspektrometrie |
|
Last Update: 2012-10-16