| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Multivariate Daten Multivariate Daten  Modellbildung Modellbildung  Multiple Regression Multiple Regression  Schätzung unbekannter Werte Schätzung unbekannter Werte |
|
| Siehe auch: MLR, MLR - Varianzanalyse | |
| Search the VIAS Library | Index | |
|
MLR - Schätzung unbekannter WerteAuthor: Hans Lohninger
Wenn man die Parameter ai der allgemeinen multiplen linearen Regressionsgleichung
 interessiert. Während die Schätzung der Standardabweichung der Parameter relativ einfach ist, ist die Berechnung der Standardabweichung von interessiert. Während die Schätzung der Standardabweichung der Parameter relativ einfach ist, ist die Berechnung der Standardabweichung von  ziemlich kompliziert. Der Grund dafür liegt in der Tatsache, dass die Verteilung von ziemlich kompliziert. Der Grund dafür liegt in der Tatsache, dass die Verteilung von  vom jeweiligen Satz der Parameter ai abhängt. Im Allgemeinen kann die multivariate Verteilungsfunktion von vom jeweiligen Satz der Parameter ai abhängt. Im Allgemeinen kann die multivariate Verteilungsfunktion von  ziemlich komplex sein. ziemlich komplex sein.
Aus diesem Grund gibt es zwei Möglichkeiten, die Standardabweichung von
Grobe Näherung:
Wir können die Standardabweichung der Residuen s verwenden, um die Standardabweichung zukünftiger Werte von y, nämlich
Exakte Lösung: Die exakte Vorgangsweise, um das Konfidenzintervall von
|
|
Home  Multivariate Daten Multivariate Daten  Modellbildung Modellbildung  Multiple Regression Multiple Regression  Schätzung unbekannter Werte Schätzung unbekannter Werte |
|
Last Update: 2012-10-08


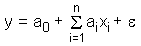
 2s kann man als grobe Näherung für die Genauigkeit des Modells nehmen (also die Genauigkeit mit der das Modell zukünftige Werte von y für konkrete x-Werte abschätzt). Die Berechnung von s ist einfach:
2s kann man als grobe Näherung für die Genauigkeit des Modells nehmen (also die Genauigkeit mit der das Modell zukünftige Werte von y für konkrete x-Werte abschätzt). Die Berechnung von s ist einfach:

