| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Univariate Daten Univariate Daten  Verteilungen Verteilungen  Einführung Einführung |
|||
| Siehe auch: Variabilität, Quantil, Parameter, Zentraler Grenzwertsatz, Box-Plots, Histogramm, Grundgesamtheit und Stichprobe, Verteilungsrechner, Normalverteilung, Signifikanzniveau, Zufallsvariable, Übung - Wahrscheinlichkeit von Beobachtungen | |||
| Search the VIAS Library | Index | |||
|
Verteilungen - EinführungAuthor: Hans Lohninger
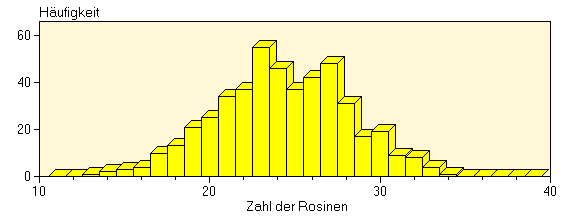
Entnimmt man nacheinander Stichproben aus demselben zufälligen Prozess, erhält man leicht voneinander abweichende Ergebnisse. Der Mittelwert dieser Ergebnisse und deren Verteilung sind normalerweise ein guter Indikator für den beprobten Prozess. Ein kurzes Beispiel soll dies verständlich machen: Nehmen Sie an, ein Physiker bäckt einen Rosinenkuchen und gibt 75 Rosinen in den Teig. Nach Rühren des Teigs und Backen des Kuchens schneidet er genau ein Drittel des Kuchens ab. Weil dieser Physiker Langeweile hat, zerbröselt er das Stück und zählt die Rosinen darin - nur 19 der zu erwartenden 25 Rosinen werden gefunden. Nun stellt sich die Frage, die den Physiker letztlich davon abhält, den Kuchen zu essen: Wie stehen die Chancen, ein Stück dieser Größe mit weniger als 20 Rosinen zu bekommen? Bevor Sie in ein statistisches Lehrbuch schauen, möchten Sie vielleicht selbst ein Experiment durchführen. Klicken Sie auf das interaktive Beispiel, um das Experiment zu starten! Sie sehen, dass die eigentliche Anzahl an Rosinen in einem Drittel des Kuchens um 25 schwankt. Das Histogramm der Häufigkeit des Vorkommens der verschiedenen Anzahlen von Rosinen könnte wie folgt aussehen:
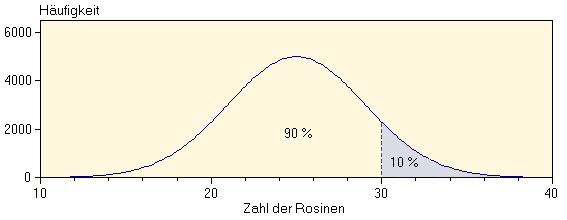
Wenn Sie den Prozess des Kuchenbackens oft genug wiederholen und Sie die Balken des Histogramms schmal genug auftragen, werden Sie schließlich eine glatte Verteilung erhalten:
Als Nächstes möchte unser Physiker wissen, wie die Chancen stehen, mehr als 30 Rosinen in dem Kuchenstück zu finden. Eine Eigenschaft von Verteilungsdiagrammen ist, dass die relative Fläche zwischen zwei Werten auf der x-Achse die Chance, dass das korrespondierende Ereignis eintritt, wiedergibt. In unserem Beispiel kann der Physiker eine vertikale Linie bei 30 Rosinen ziehen. Die relative Fläche oberhalb dieser Markierung gibt die Chance, mehr als 30 Rosinen im Kuchenstück zu finden, an (was anhand der Verteilungskurve ungefähr 10 % ist).
Manchmal ist es schwer, die relative Fläche zu bestimmen. Dann sollte man die Verteilungskurve so skalieren, dass sie eine Fläche von exakt 1.0 hat. Die Fläche unterhalb der Kurve stellt die Chance, dass ein Ereignis in diesen Bereich fallen kann, dar. Diese Kurve wird Wahrscheinlichkeitsdichtefunktion (engl. probability density function, pdf) genannt: 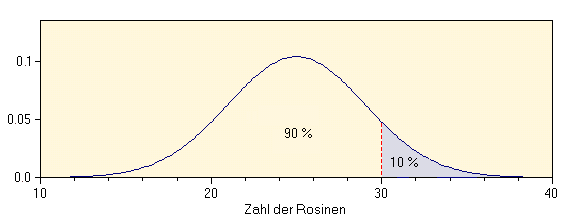
|
|||
Home  Univariate Daten Univariate Daten  Verteilungen Verteilungen  Einführung Einführung |
|||
Last Update: 2021-08-15